이 글은 포스텍 성효진 교수님의 이종병렬컴퓨팅(CSED490C) 강의를 기반으로 재구성한 것입니다.
이 글에서는 parallel scan (prefix sum)과 koggle-stone algorithm(work-inefficient)와 brent-kung(work-efficient) algorithm을 살펴본다.
Scan
Inclusive Scan
어떤 binary associative operator ⊕와 array [x$_0$, x$_1$, ... , x$_{n-1}$]에 대해, [x$_0$, x$_0$ ⊕ x$_1$, ... , (x$_0$ ⊕ x$_1$ ⊕ ... ⊕ x$_{n-1}$]을 리턴하는 것이 inclusive scan이다.
scan은 radix sort, quick sort, 등등 다양한 병렬 알고리즘에 사용되며, 그냥 prefix sum이라고 생각하면 된다.
일반적으로 parallel한 버전을 만들 때, 각 thread는 출력 값을 어디에 쓸 지 알아야 한다. scan의 경우 각 thread는 다른 thread가 쓰는 값에 의존하기 때문에 이를 고려해서 효율적인 병렬 알고리즘을 만들어야 한다.
exclusive scan
어떤 binary associative operator ⊕와 array [x$_0$, x$_1$, ... , x$_{n-1}$]에 대해, [, x$_0$, ... , (x$_0$ ⊕ x$_1$ ⊕ ... ⊕ x$_{n-2}$]을 리턴하는 것이 exclusive scan이다.
inclusive scan과 조금 다르다. inclusive scan은 i번째 결과값이 i번째 element의 연산을 포함하는데, exclusive scan은 i번째 결과값이 i번째 element와의 연산을 포함하지 않는다.
- 예를 들어 inclusive scan은 처음 값이 0이 아니라 arr[0]인데, exclusive scan은 0부터 시작한다. 끝 값도 조금 다르다. inclusive scan의 arr[n-1]은 모든 배열의 합인데, exclusive scan의 arr[n-1]은 모든 배열의 합 - arr[n-1]이다.
exclusive scan을 사용하는 이유는 할당된 buffer의 시작 주소를 찾을 때와 같은 상황에서 사용한다. inclusive scan이나 exclusive scan은 변환하기가 매우 쉽다!
Inclusive Sequential Scan
input [x0, x1, x2, ...]에 대해 output [y0, y1, y2, ...]를 계산한다고 했을 때,
- y$_0$ = x$_0$
- y$_1$ = x$_0$ + x$_1$
- y$_2$ = x$_0$ + x$_1$ + x$_2$
- ...
- 즉, y$_i$ = y$_{i-1}$ + x$_i$
따라서 prefix sum의 sequential 버전은 다음과 같다. 이 경우 시간복잡도는 O(n)이다.
y[0] = x[0]
for(int i = 1; i < len; i++){
y[i] = y[i-1] + x[i];
}
Parallel Inclusive Scan
제일 쉬운 버전은, y element 하나를 계산하기 위해 필요한 모든 x 값들을 다 더하면 된다. 성능을 신경쓰지 않는다면 병렬 구성 자체는 쉽다. 그러나 이는 O(n$^2$)의 연산이 필요하기 때문에 다른 방법을 살펴본다.
Kogge-Stone Parallel Scan Algortihm
각 output element를 이전 element의 reduction으로 계산하는 방식이다. 이 때 이전에 계산했던 reduction partial sum은 output element를 계산할 때 사용된다. kogge-stone tree를 기반으로 한 계산 방식이다.
- global memory에서 size n의 배열 T를 shared memory로 load한다. 이 때 n은 2의 k승이라고 하자.
- pass를 logn번 반복하며, 각 pass에서 stride를 1부터 n/2까지 증가시킨다.
- 이 때 각 pass에서는 stride부터 n-1개의 thread가 active하다.
- 예를 들면 pass 0에서는 stride가 1이다. 1부터 n-1까지의 thread가 active하다.
- 이후 간격이 stride인 pair element를 더한다.
- 이 때 각 pass에서는 stride부터 n-1개의 thread가 active하다.
- shared memory의 결과로부터 global memory로 값을 쓴다.
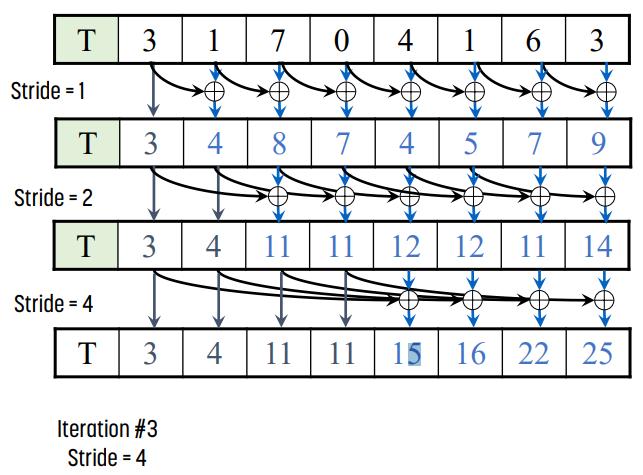
위 예시는 size 8일 때 3번의 pass를 보여준다.
- pass 1에서는 stride가 1이므로 인접한 값을 더한다.
- pass 2에서는 stride가 2이므로 2칸 옆에 있는 값을 더한다.
- pass 3에서는 stirde가 4이므로 4칸 옆에 있는 값을 더한다.
예시를 잘 보면 알겠지만, 최종 결과물에서 i번째 값은 0 ~ i번째 값이 모두 더해지는 것을 확인할 수 있다.
CUDA kernel
__global__ void koggeStoneScan(float* X, float* Y, int n) {
__shared__ float XY[SECTION_SIZE];
int i = blockIdx.x*blockDim.x + threadIdx.x;
XY[threadIdx.x] = (i < n) ? X[i] : 0;
float temp = 0.f;
for (unsigned int stride = 1; stride < blockDim.x; stride *= 2) {
__syncthreads(); // __syncthread();
if (threadIdx.x >= stride) {
temp = XY[threadIdx.x] + XY[threadIdx.x - stride];
}
__syncthreads(); // __syncthread();
if (threadIdx.x >= stride)
XY[threadIdx.x] = temp;
}
if (i < n)
Y[i] = XY[threadIdx.x];
}
이 코드에서 temp 값을 사용하는 이유는, shared memory에 바로 값을 쓰면 input 값이 바뀌기 때문이다. 때문에 temp에 값을 쓰고 이후에 다시 shared memory에 값을 쓴다.
`__syncthread()`가 2군데에 있는데, 2번째에 있는 `__syncthread()`를 삭제하면 다른 thread가 같은 위치에 대해 동시에 쓸 수 있기 때문에 필요하다.
Double Buffering
위 코드에서는 2개의 bariier를 사용했는데, 이를 해결하기 위해 double buffering을 사용한다.
- T0와 T1의 사본을 사용한다.
- T0을 input으로, T1을 output으로 사용한다.
- 이후 각 pass에서 input/output의 역할을 바꾼다. 예를 들어 iteration 0에서는 T0가 input, T1이 output, iteration 2에서는 T1이 input, T0가 output이 되는 방식이다.
일반적으로 2개의 pointer를 사용해 source와 destination을 swap()하는 방식으로 사용한다. 이를 통해 위 코드에서 2번째 barrier를 없앨 수 있다.
Double-Buffered Kogge-Stone Parallel Scan


이렇게 하면 오직 하나의 barrier만 사용하고, destination에 값을 쓰면 source의 값이 바뀌지 않음을 보장할 수 있다.
효율 분석
이 scan 방식은 logn번의 iteration을 수행한다. 각 iteration은 n-1번, n-2번, n-4번, ... n-n/2번의 add 연산을 수행한다. 따라서 총 add operation의 개수는 n * logn - (n-1) = O(nlogn)이다.
따라서, 이 방식은 work-inefficient한 방식이다. sequential 방식이 O(n)임을 생각해 보면 된다.
따라서, 낮은 work efficiency로 인해 resource가 가득 찼을 때 parallel 알고리즘이 sequential보다 더 느릴 수도 있다.
Brent-Kung Algorithm
이 방식은 work-efficient이다.
balanced tree 방식의 parallel algorithm pattern을 사용해 효율을 올린다. input data에 대해 balanced binary tree를 만들고, root부터 tree를 sweeping한다.
이 때 tree는 실제 data structure가 아니라 각 pass에서 thread가 작업을 결정할 때 사용하는 개념이다.
scan의 경우, 1) leaf에서 root까지 내려가면서 tree의 internel node들의 partial sum을 구성한다. 그러면 root는 모든 leaf node들의 합을 가지게 된다. 2) 이후 root부터 leaf까지 올라가면서 계산해 둔 partial sum을 사용해 계산하지 않은 scan 값을 계산하는 방식이다.

위 그림처럼 leaf부터 root까지 올라가면서 internal node들의 partial sum을 계산한다.
위 예시에서는 x7이 모든 값의 합을 가지고 있게 된다. 반면 다른 값들은 아직 완벽한 값을 가지고 있지 않다.
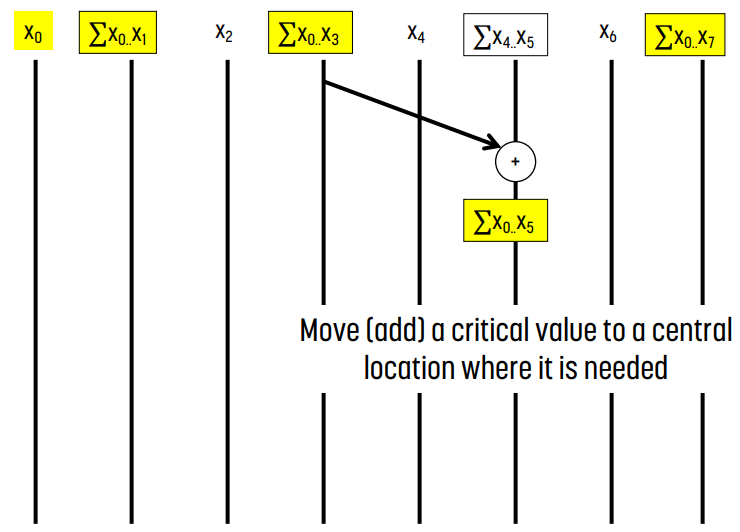

post scan step에서는 계산된 값들의 일부를 이용해 아직 계산되지 않은 위치의 값을 쉽게 계산할 수 있다.
예를 들어 왼쪽 그림에서 x0부터 x5까지 값을 구하고 싶다면 x0부터 x3까지의 합이 들어 있는 x3과, x4부터 x5까지의 합이 들어 있는 x5를 더하면 된다.
같은 방식으로 오른쪽 그림에서 x0부터 x2까지의 합을 구하고 싶다면 x0부터 x1까지의 합이 들어 있는 x1과 x2를 더하면 된다.
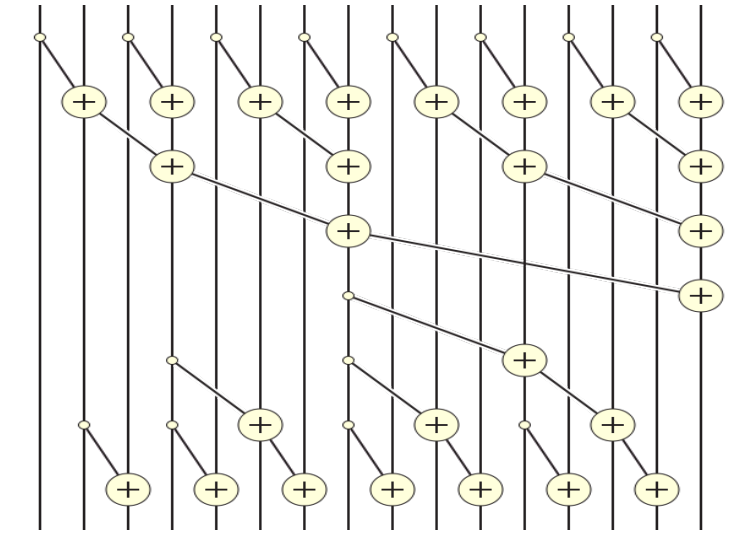
즉 위와 같은 방식으로 1) reduction을 통해 partial sum을 구하고 2) 이 값들을 사용해 다시 prefix sum을 계산한다.
CUDA Kernel
__global__
void brentKungScan(float* X, float* Y, int n) {
__shared__ float XY[SECTION_SIZE];
int i = 2*blockIdx.x*blockDim.x + threadIdx.x;
if (i < n)
XY[threadIdx.x] = X[i];
if (i + blockDim.x < n)
XY[threadIdx.x + blockDim.x] = X[i + blockDim.x];
// reduction phase
for (unsigned int stride = 1; stride <= blockDim.x; stride *= 2) {
__syncthreads();
int index = ((threadIdx.x + 1) * stride * 2) - 1;
if (index < SECTION_SIZE) {
XY[index] += XY[index - stride];
}
}
// post scan phase
for (unsigned int stride = SECTION_SIZE/4; stride > 0; stride /= 2) {
__syncthreads();
int index = ((threadIdx.x + 1) * stride * 2) - 1;
if (index + stride < SECTION_SIZE) {
XY[index + stride] += XY[index];
}
}
__syncthreads();
if (i < n)
Y[i] = XY[threadIdx.x];
if (i + blockDim.x < n)
Y[i + blockDim.x] = XY[threadIdx.x + blockDim.x];
}
예시를 보자. 예를 들어 input size가 8일 때, reduction step에서, stride가 1이면 threadIdx.x + 1은 1, 2, 3, 4, 5, 6, 7, 8이 된다. 그러면 index는 1, 3, 5, 7, 9, 11, 13, 15가 된다. `XY[index] += XY[index - stride]`를 하므로 reduction이 올바르게 계산된다.
한편, 이 때 post scan step에서 bank conflict가 발생할 수도 있다.
효율 분석
parallel inclusive scan은 2 * logn번의 pass를 실행한다. logn번은 reduction에서, logn번은 post scan에서 사용한다.
각 iteratioon에서는 n/2, n/4, ... , 1번, 그리고 1, 2, ... , n/4, n/2번의 add operation을 수행한다. 따라서 add operation은 총 2(n-1)번 수행하므로 O(n)이다.
parallel 버전에서 추가된 add operation의 회수는 sequential 버전의 2배 이하이다. 이 경우, parallel하게 계산하는 경우 2배로 늘어난 연산으로 인한 overhead는 쉽게 극복할 수 있다.
Kogge-Stone vs Brent-Kung
brent-kung은 kogge-stone과 비교했을 때, 절반의 thread를 사용한다. brent-kung의 경우 각 thread는 2개의 element를 shared memory로 load하기 때문이며, reduction이기 때문에 필요한 thread의 개수가 훨씬 적다.
brent-kung은 kogge-stone과 비교했을 때 pass의 개수가 2배이다.
즉, brent-kung의 경우 1/2배의 thread, 반면 2배의 pass -> n/2 * 2logn = nlogn이므로, GPU에서 효율성은 비슷하다. 그러나 pass의 개수가 더 많은데, 각 pass의 실행은 이전 pass의 결과에 dependent하기 때문에 더 많은 barrier가 필요하므로, 더 많은 synchronization overhead를 발생시킨다. 때문에 GPU의 block 내부의 parallel scan은 kogge-stone이 더 좋다.
일반화
매우 큰 input에서 hierarchical parallel scan
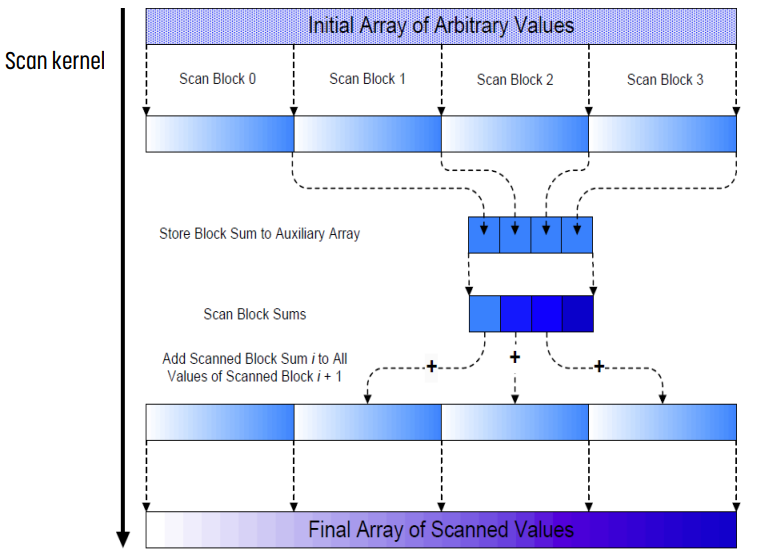
매우 큰 reduction에 대해, 각각을 section으로 나누고, section의 결과를 다시 reduction 했던 것처럼, scan 또한 같은 방식으로 진행한다. section의 결과를 auxiliary array에 넣고, 그 array를 다시 scan한다. 이후 최종 결과를 얻을 수 있다.
global memory content 사용하기
하나의 thread block에 속한 shared memory나 register 값은 다른 thread block에 보이지 않는다. 때문에 data를 visible하게 만들기 위해서는 data가 global memory에 쓰여야 한다.
그러나, global memory에 써진 값들은 memory fense로 인해 보이지 않는데, kernel 실행이 종료되었을 때 fense가 사라진다. 따라서 한 kernel의 실행이 끝났을 때 다른 kernel을 실행해야 한다. 그래야만 종료된 kernel이 global memory에 쓴 값이 다른 thread block에서 보인다.
임의 길이 input에 대해 작업하기
- `2 * blockDim.x`개의 element를 처리할 수 있는 scan kernel을 만든다. kogge-stone의 경우, 각 section이 blockDim.x개의 element가 하나의 block에 할당되게 만든다.
- 각 block은 sum[blockIdx.x]에 값을 쓴다.
- sum array에 대해 parallel scan을 다시 실행한다. 만약 block size보다 sum 배열의 크기가 훨씬 크다면 sum을 나눠야 할 것이다.
- scan된 sum 배열의 값을 해당 section의 element에 더한다.
CUDA kernel : exclusive scan
kogge-stone kernel의 경우,
thread block 0에서 thread 0은 shared memory에 값을 올릴 때 `arr[0]`이 아니라 `0`을 올리게 한다. 다른 모든 thread들은 `X[threadIdx.x - 1]`을 `XY[threadIdx.x]`에 쓴다.
다른 모든 thread block들은 `X[(blockIdx.x * blockDim.x) + threadIdx.x - 1]`을 `XY[threadIdx.x]`에 쓴다.
brent-kung의 경우도 매우 유사하지만, 각 thread가 2개의 element를 load할 수 있어야 한다. 제일 앞의 0이 load되어야 하고, 다른 모든 element들은 단 한 칸만 shift되어야 한다.
잘못된 내용이나 오탈자에 대한 지적, 질문 등은 언제나 환영합니다.
'CS > Parallel Computing' 카테고리의 다른 글
| [이종병렬컴퓨팅] OpenMP (0) | 2023.12.17 |
|---|---|
| [이종병렬컴퓨팅] Parallel Patterns : Sparse Computation (1) | 2023.12.17 |
| [이종병렬컴퓨팅] Parallel Patterns : Reduction (0) | 2023.12.16 |
| [이종병렬컴퓨팅] Parallel Patterns : Histogram (0) | 2023.12.16 |
| [이종병렬컴퓨팅] Parallel Patterns : Convolution (0) | 2023.10.28 |
![[이종병렬컴퓨팅] Parallel Patterns : Scan](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbDayZA%2FbtsB7nEi0b2%2FNfaIHNTYpTJUPwAxUK0cF1%2Fimg.png)