이 글은 포스텍 성효진 교수님의 이종병렬컴퓨팅(CSED490C) 강의를 기반으로 재구성한 것입니다.
이 글에서는 다음과 같은 내용을 다룬다.
- convolution과 tiled convolution : 1D/2D convolution과 tiled convolution (input tiling, output tiling)
- 2D convolution kernel을 작성하는 방법 : boundary condition 처리
- tiled parallel convolution 알고리즘의 cost와 장점
Convolution
인접한 input data element의 weighted sum 연산. 이 때 weighted sum 연산에 사용하는 weight를 input mask array 또는 convolution kernel 또는 filter라고 부른다.
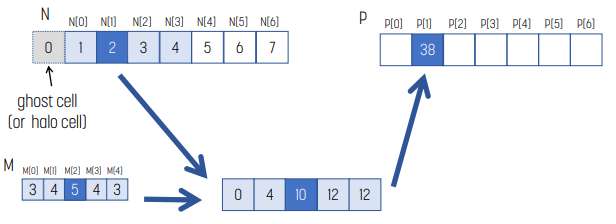
예시 : 1D Convolution

위 예시는 input arrya가 N, convolution mask가 M일 때 P[2]를 계산하는 방법을 나타낸다.
- convolution mask size가 5이므로, N의 P[2]를 포함해 주변의 5개 element를 가져온다.
- 두 vector를 내적한다.
- 내적한 결과의 합을 P[2]에 넣는다.
수식으로 표현하면, P[2] = N[0] * M[0] + N[1] * M[1] + N[2] * M[2] + N[3] * M[3] + N[4] * M[4]이다.
Boundary Condition
그러나 위 그림처럼 input array의 끝에 가까운 경우 convolution mask의 크기와 맞지 않은 boundary condition이 생긴다. 이 경우, input array의 범위를 벗어나는 것을 ghost element라고 한다. ghost element는 applicatoin마다 처리하는 방식이 다르다. 0이 들어갈 수도 있고, boundary에 있는 값을 복사하기도 한다.
위 예시는 ghost element에 0을 넣는 경우이다.
코드 : 1D convolution
__global__ void convolution1D_basic(float* N, float* M,
float* P, int Kernel_Width, int Width)
{
int i = blockIdx.x*blockDim.x + threadIdx.x;
float Pvalue = 0.f;
int N_start_point = i - (Kernel_Width/2);
for (int j = 0; j < Kernel_Width; j++) {
if (N_start_point + j >= 0 && N_start_point + j < Width)
Pvalue += N[N_start_point + j] * M[j];
}
if (i < Width)
P[i] = Pvalue;
}1D convolution을 수행하는 kernel code는 위와 같다.
9번줄의 if문은 boundary condition을 확인하는 부분이다.
2D Convolution
그러면 2D의 경우를 보자. 사실상 1D와 동일하다!

위 예시는 2D convolution 예시이다. 1D와 동일한 방식으로, 특정 element를 convolution하기 위해 해당 element 주변의 element와 convolution mask를 내적하고 합계를 결과에 넣는다.
예시 : 2D Convolution Boundary Check

2D의 경우 ghost cell 처리하는 방식은 1D와 동일하다.
Convolution Mask의 Access Pattern
convolution mask는 다음과 같은 특징이 있다.
- 크기는 일반적으로 작다.
- kernel 실행 중에 바뀌지 않는다.
- 모든 output을 계산하기 위해 필요하며, 접근하는 순서가 동일하다.
따라서 convolution mask는 constant memory에 넣기 좋다!
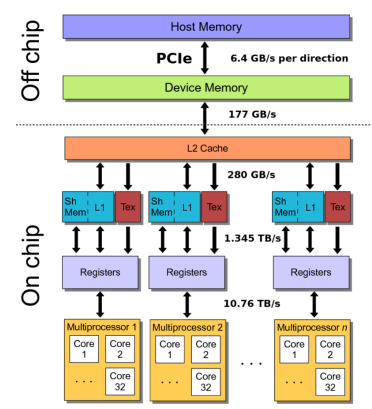
각 thread는 grid별 constant memory나 texture memory에 100 cycle만에 read only할 수 있으며 cache hit인 경우 10 cycle만에 read only할 수 있다.
Constant Memory
constant memory는 `cudaMemcpyToSymbol()`을 사용해 device memory에 복사한다. device로 옮겨지는 다른 변수와 같은 방식이다. `cudaMemcpyToSymbol()`는 해당 변수가 수정되지 않으며, read only로 안전하게 caching된다는 것을 알려준다.
#define MAX_MASK_WIDTH 10
// global variable, outside any kernel/function
__constant__ float M[MAX_MASK_WIDTH];
// allocate N, P, initialize M_h and N, copy N to N_d
…
cudaMemcpyToSymbol(M, M_h, MASK_WIDTH*sizeof(float));
// Mask is not given as an argument
convolution_1D_basic_kernel<<<dimGrid, dimBlock>>> (N_d, P_d, MASK_WIDTH, Width);
Constant Cache
constant cache는 kernel 실행 중에 수정되지 않는 constant data를 위한 특별한 cache이다. `__constant__`로 선언하며, L1 cache와 비슷한 throughput으로 constant cache에 접근할 수 있다.
또한, constant cache는 read only이므로 warp 내의 같은 주소에 접근할 때 동시에 제공된다.
추가적으로 read only이므로 coherence에 대해 신경쓰지 않아도 된다.
1D Tiled Convolution
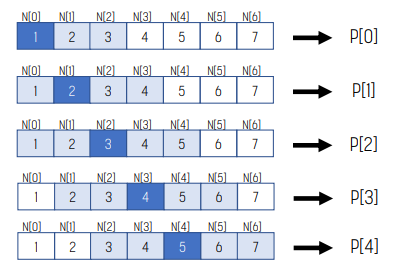
인접한 output element는 같은 input element를 공유한다. 따라서 모든 thread의 input element를 shared memory에 올려 global memory access를 줄일 수 있다.
위 예시에서 mask_width가 5일 때 N[2]는 P[0], P[1], P[2], P[3], P[4]에서 사용하는 변수를 사용한다.

각 group이 T개의 output element를 계산한다고 하자.
- T개의 output element를 계산하기 위해 T + mask_width - 1개의 input element가 필요하다.
- 일반적으로 T는 mask_width보다 훨씬 크다.
Tiling Option


tiling하는 방법은 크게 2가지가 있다.
- output tile에 thread block 크기를 맞추는 방법
- 모든 thread가 output element 계산에 참가한다. 위 예시에서는 blockDim.x가 4이다.
- 몇몇 thread는 input element를 shared memory에 올려야 한다.
- input tile에 thread block 크기를 맞추는 방법
- 몇몇 thread는 output element 계산에 참가하지 않는다. 위 예시에서는 blockDim.x가 8이다.
- 각 thread는 1개의 input element를 shared memory에 올린다.
여기서는 두 번째 방법을 살펴본다!
Input/Output Data와 Thread의 매핑
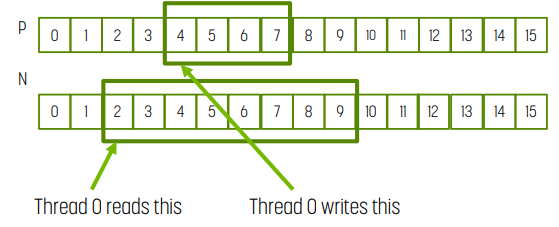
N이 input, P가 output이다.
- 각 thread에서 index_input = index_output - (mask_width/2)이다.
- tile_width은 tile의 output element 개수. 위 예시에서는 4.
- thread block size은 tile_width + (mask_width - 1). 위 예시에서는 8.
코드
float output = 0.0f;
__shared__ float Ns[tile_width + (mask_width – 1)];
int tx = threadIdx.x;
int index_output = blockIdx.x * blockDim.x + threadIdx.x;
int index_input = index_output – (mask_width – 2);
if (index_input >= 0 && index_input < width)) {
Ns[threadIdx.x] = N[index_input];
}
else {
Ns[threadIdx.x] = 0.0f;
}
if (tx < tile_width) {
output = 0.0f;
for (int j=0 ; j < mask_width; j++) {
output += M[j] * Ns[tx + j];
}
P[index_output] = output;
}위에서 언급했듯 input tile에 thread block의 크기를 맞추는 방법이기에 각 thread는 하나의 input element를 shared memory에 올려야 한다. 위 코드의 8번줄부터 13번줄까지 shared memory에 input memory를 올리는 모습이다.
15번줄부터는 0부터 (tile_width-1)까지의 thread만 계산에 참가하는 것을 보여준다.
해석

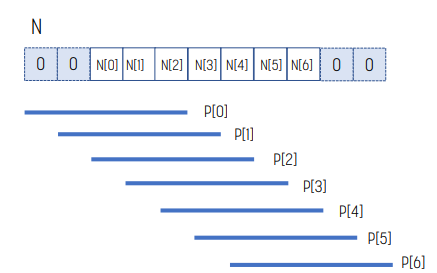
mask_width가 5인 상황이다.
- NS[0]은 thread 1에 의해 사용된다.
- NS[1]은 thread 1, 2에 의해 사용된다.
- NS[2]은 thread 1, 2, 3에 의해 사용된다.
- NS[3]은 thread 1, 2, 3, 4에 의해 사용된다.
- NS[4]은 thread 1, 2, 3, 4에 의해 사용된다.
- NS[5]은 thread 1, 2, 3에 의해 사용된다.
- NS[6]은 thread 1, 2에 의해 사용된다.
- NS[7]은 thread 1에 의해 사용된다.
2D Convolution
Padding

2D matrix를 DRAM에서 burst할 때, width가 burst의 배수가 아닌 경우 misalignment가 발생할 수 있다. 때문에 width를 burst의 배수에 맞춰 row의 시작점을 DRAM burst에 맞추는 방식이 좋다. 이는 width에 추가적인 padding을 넣는 방식이다.
만약 위 예시에서 padding이 없는 상황을 가정해 보자. 이 때 burst는 4개의 element를 가져온다고 하자.
그러면 M$_1, _0$은 burst 0에 속해 있고, M$_1, _1$과 M$_1, _2$는 burst 2에 속해 있기에 row 1을 가져오기 위해 DRAM access를 2번 해야 한다.
반면 padding이 있다면 1번만 DRAM access해도 된다.
Tiling Strategy
Tile 설계
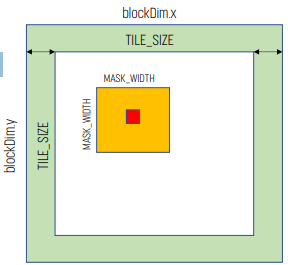
- thread block을 input tile에 매핑한다. 그러면 모든 thread는 N의 tile을 shared memory에 올린다. 그러면 thread들은 N의 element를 사용해 P를 계산한다.
- TILE_SIZE는 x, y축의 output tile 크기를 정의한다.
- thread block size는 TILE_SIZE와 input tiling의 mask width에 의존한다.
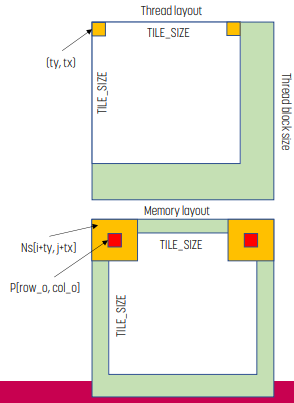
Indexing
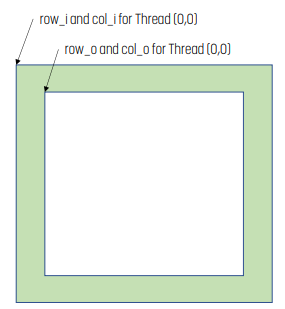
int tx = threadIdx.x;
int ty = threadIdx.y;
int row_o = blockIdx.y * TILE_SIZE + ty;
int col_o = blockIdx.x * TILE_SIZE + tx;
int row_i = row_o – MASK_WIDTH/2;
int col_i = col_o – MASK_WIDTH/2;그러면 input/output index는 위 코드와 같다. input의 경우 ghost cell을 포함해야 하기에 output보다 더 크다.
Shared Memory에 Input Tile Load
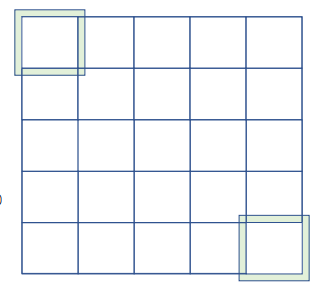
float output = 0.0f;
if ((row_i >= 0) && (row_i < N.height) && (col_i >= 0) && (col_i < N.width)) {
Ns[ty][tx] = N[row_i*N.width + col_i];
}
else {
// threads that load halos outside N returns 0.0
Ns[ty][tx] = 0.0f;
}input tile을 shared memory에 올리는 코드는 위와 같다. 범위가 벗어나는 경우 ghost element이므로 if-else를 사용한다.
Output 계산
float output = 0.0f;
if (ty < TILE_SIZE && tx < TILE_SIZE){
for (i = 0; i < MASK_WIDTH; i++) {
for (j = 0; j < MASK_WIDTH; j++) {
output += M[i][j] * Ns[i+ty][j+tx];
}
}
if (row_o < P.height && col_o < P.width)
P[row_o * P.width + col_o] = output;
}3번줄의 첫 번째 if문은 TILE 안에 있는 thread만 수행하게 만든다. thread block size가 TILE_SIZE보다 크기 때문에 필요하다.
9번줄의 if문은 output이 올바른 범위 내에 있는지 확인한다.
Bandwidth Reduction 분석
1D Convolution의 경우
TILE_SIZE + MASK_WIDTH - 1개의 element가 shared memory에 올라간다.
TILE_SIZE * MASK_WIDTH번의 global memory access가 shared memory access로 바뀐다.
따라서 bandwidth reduction은 다음과 같다.
$\frac{\text{(TILE_SIZE * MASK_WIDTH)}}{\text{(TILE_SIZE + MASK_WIDTH - 1)}$
위 수식은 edge tile에 있는 ghost cell을 무시한 수식이다.
Ghost Cell을 고려한 경우
boundary tile의 예외를 처리하기 위해 TILE_SIZE + $\frac{\text{(MASK_WIDTH - 1)}}{2}$개의 element를 shared memory에 올렸다.
이 때, ghost cell들에 대해서는 global memory access를 하지 않았다. 그만큼 더 줄어든다.
일반화
일반화하면, MASK_WIDTH << TILE_WIDTH인 경우 MASK_WIDTH에 근사하게 bandwidth가 줄게 된다.
예시

mask_width가 5인 위 예시에서, 각 P의 element를 계산하기 위해 5개의 N element가 있어야 한다. tiling을 쓴 경우, 5개의 N element는 shared memory에 있는 것을 참조한다.
shared memory에는 12개의 element가 올라갔으며, 전체 output tile을 위해 8 * 5개의 shared memory access를 했다. 따라서 bandwidth reduction은 40/12 = 3.3으로, 3.3배 향상되었다.
boundary tile까지 고려해 보자. boundary가 아닌 element는 10개가 shared memory에 올라간다. 이 떄 ghost cell들은 global memory access를 하지 않으니, 전체 access 회수는 3 + 4 + 6*5 = 37이다. 따라서 37 / 12로, 3.7배 향상되었다.
2D Convolution의 경우
(TILE_SIZE + MASK_WIDTH - 1)$^2$개의 element가 shared memory에 올라간다.
P의 각 element를 계산하기 위해 MASK_WIDTH$^2$개의 N element에 접근해야 하므로 TILE_SIZE$^2$ * MASK_WIDTH$^2$번의 global memory access가 발생한다.
따라서 bandwidth reduction은 다음과 같다.
$\frac{\text{TILE_SIZE}^2 \times \text{MASK_WIDTH}^2}{\text{(TILE_SIZE + MASK_WIDTH - 1)} ^ 2}$
위 수식은 edge tile에 있는 ghost cell을 무시한 수식이다.
TILE_SIZE에 비례해 memory bandwidth가 급격하게 줄게 된다. 근사하면 TILE_SIZE$^2$배만큼 성능이 향상되기 때문이다.
그렇지만 TILE_WIDTH가 커질수록 필요한 shared memory size가 더 커진다는 것을 인지해야 한다.
이외의 최적화
Texture Memory 사용
- input image를 shared memory 대신 texture cache에 올리기
- 코드가 더 쉽고 깔끔해지며, texture hardware path를 통해 global memory read를 할 수 있다.
- 이 경우 data read는 2D/3D spatial locality에 특별화된 texture cache에 저장된다.
- CUDA array 사용
- global memory에 1D/2D/3D 형태의 data 저장을 위한 object를 만든다.
- OpenGL이나 DirectX의 표준 교환 형식이다.
host code
// global declaration of 2D float texture (visible for host and device code)
texture<float, cudaTextureType2D, cudaReadModeElementType> tex; …
// Create explicit channel description (could use an implicit as well)
cudaChannelFormatDesc channelDesc = cudaCreateChannelDesc(32, 0, 0, 0, cudaChannelFormatKindFloat);
// Allocate CUDA array in device memory
cudaArray* cuArray;
cudaMallocArray(&cuArray, &channelDesc, width, height);
// Copy some data located at address h_data in host memory into CUDA array
cudaMemcpyToArray(cuArray, 0, 0, h_data, size, cudaMemcpyHostToDevice);
…
// Bind the array to the texture reference
cudaBindTextureToArray(tex, cuArray, channelDesc);texture data storage를 할당하고, texture를 해당 data storage에 할당한다.
- device code
float value = tex2D(tex, xpos, ypos);texture reference를 사용해 data fetch할 수 있다.
Loop Unrolling
loop를 펼쳐서 control flow overhead를 줄이는 방식. 이 방법을 사용하면 global read 성능이 향상될 수 있다.
예를 들어 숫자 1개 대신 4개의 숫자를 가져오던가(memory coalescing), float4 vector type을 쓰면 locality와 bandwidth 최적화에서 이점이 있다.
Matrix Multiplication
입력 image를 matrix로 바꾸고, matrix multiplication을 수행한다.
기본적으로 convolution은 filter와 이동하는 window에 의해 선택된 local region 사이의 내적이므로 memory에 있는 모든 window를 확장하고 matrix multiplication으로 최적화 할 수 있다.
- 예를 들어 input image f가 [1, 2, 3, 4]rh filter가 [-1, -2, -3]인 경우,
- f = $ \begin{bmatrix} 1 & 2 & 3 \\ 2 & 3 & 4 \\ \end{bmatrix}$, g = $\begin{bmatrix} -1 \\ -2 \\ -3 \end{bmatrix}$로 설정하고 matrix multiplication하면 된다.
Computational Transformation
algorithmic strength reduction을 통해 multiplication 연산 회수를 줄일 수 있다. 예를 들어 덧셈같은 weak operation의 회수를 늘이고 곱셈같은 strong operation의 회수를 줄일 수 있다.
- Winograd
- Strassen Algorithm : 행렬 곱을 부분으로 나눠, 8번의 곱연산을 7번의 곱연산과 n번의 덧셈으로 나누는 기술이다.
- Fast Fourier Transform
잘못된 내용이나 오탈자에 대한 지적, 질문 등은 언제나 환영합니다.
'CS > Parallel Computing' 카테고리의 다른 글
| [이종병렬컴퓨팅] Parallel Patterns : Reduction (0) | 2023.12.16 |
|---|---|
| [이종병렬컴퓨팅] Parallel Patterns : Histogram (0) | 2023.12.16 |
| [이종병렬컴퓨팅] Performance Considerations (0) | 2023.10.28 |
| [이종병렬컴퓨팅] Thread Execution Efficiency (0) | 2023.10.28 |
| [이종병렬컴퓨팅] Memory와 Data Locality - Tiled Multiplication & Unified Memory (0) | 2023.10.27 |
![[이종병렬컴퓨팅] Parallel Patterns : Convolution](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FntmHl%2FbtsziQp2A3G%2FHstLK7Qjjx7r9oHwlJTHCK%2Fimg.png)