이 글은 포스텍 성효진 교수님의 이종병렬컴퓨팅(CSED490C) 강의를 기반으로 재구성한 것입니다.
이 글에서는 memory bandwidth를 절감가힉 위한 parallel sparse computation에서 input data를 압축하는 방법을 살펴본다. 이를 통해 memory의 utilization을 높일 수 있고, on-chip memory로 전송되는 data 크기를 줄일 수 있다.
또한 clamping으로 variation 제한, sorting, transposition 등으로 불규칙한 데이터를 규칙적으로 만드는 방법을 살핀다.
Sparse Matrix
자연 상태의 많은 system들은 sparse하다. 보통 matrix의 80% 이상이 0이면 sparse matrix라고 한다.
Sparse Matrix-Vector Multiplication, SpMV

sparse matrix-vector multiplication는 많은 곳에서 사용되는데, 예를 들어 계수행렬 A, vector x, y에 대해 linear system Ax = y의 역행렬을 구해야 할 때 사용된다.
sparse linear system 해결
- sparse matrix vector multiplication을 기반으로 하는 iterative conjugate gradient solver가 일반적인 방법이다.
- mv(A)가 A와 matrix-vector 곱을 계산할 때 시간복잡도일 때, O(mv(A) * n)의 시간이 걸린다.
- 이 경우 SpMV operation에 대해 100초 이상이 걸린다.
신경쓸 것들
dense matrix multiplication과 비교했을 때 SpMV은 불규칙하고, 구조화되지 않는다. 또한 input data reuse가 거의 없고, compiler transformation tool로 이득을 얻기 힘들다.
때문에 성능을 높이기 위해서는 divergence나 load imbalance를 줄여 regularity를 최대화하거나, layout을 재배열해 DRAM burst utilization을 최대화하는 방법이 있다.
Sparse Matrix Format

왼쪽으로 갈수록 구조화된 것, 오른쪽으로 갈수록 구조가 없는 것이다. 이 글에서는 ELL, CSR, HYB, COO, JDS 정도만 살펴본다.
간단한 Parallel SpMV

각 thread가 하나의 row를 처리하면 된다. 이걸 이제부터 발전시켜 나갈 것이다.
Compressed Sparse Row Format : CSR

위 형식은 compressed sparse row format이다. non-zero element에 대한 정보만 저장한다.
- data[] : 값들을 저장한다. length는 matrix에서 non-zero element의 개수와 동일하다.
- col_index[] : column index를 저장한다. length는 non-zero element의 개수와 동일하다.
- row_ptr[] : 각 row에 non-zero element의 개수가 몇개인지 prefix sum 형태로 저장된다. length는 row + 1과 동일하다.
예시


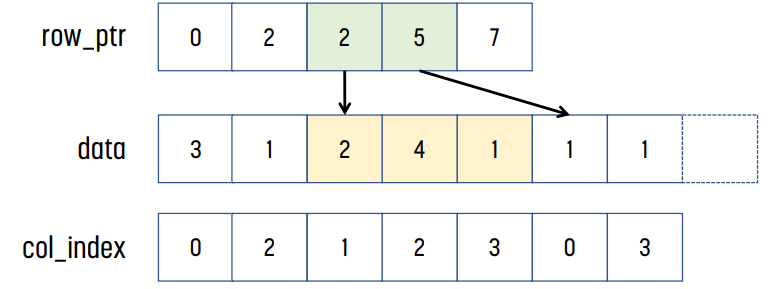
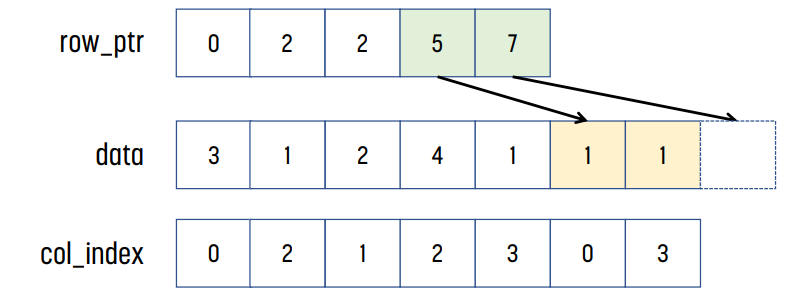
위 예시의 경우, row 0에는 3, 1이, row 1에는 아무것도 없고, row 2에는 2, 4, 1이, row 3에는 1, 1이 있다.
row_ptr[0]은 0이고, row_ptr[1]은 row 0까지 non-zero element의 개수는 2이므로 2이다. row_ptr[2]는 row 1까지 non-zero element의 개수이므로 2이다. 같은 방식으로, row_ptr[2] = 5, row_ptr[3] = 7이다.
이후 col_index를 보면 된다. row_ptr[1]까지 element가 2개이므로, data와 col_index의 index 0과 index 1이 row 0에 대한 정보를 가지고 있다는 것을 알 수 있다. 같은 방식으로, row_ptr[1]이 2이고 row_ptr[2]의 값이 2이므로, row 1에는 non-zero 값이 없다는 것을 알 수 있다. 똑같이 row_ptr[2]가 2, row_ptr[3]이 5이므로 row 2에는 non-zero element가 3개 있다는 것을 알 수 있고, index 2, 3, 4에 해당 element들이 저장된다.
이게 CSR format이다.
Compressed Sparse Row Kernel Design
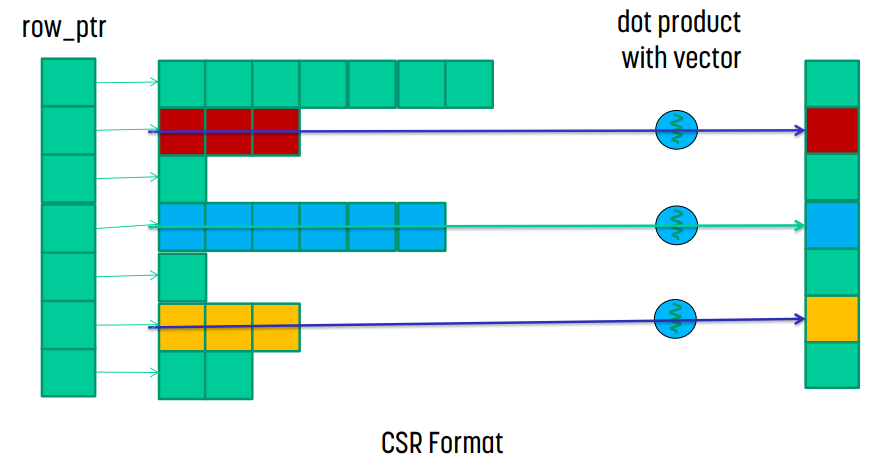
CSR format의 경우, row_ptr과 data를 사용해 어떤 row에 어떤 data가 있는지 알 수 있다. 그렇다면 vector와 이 값을 dot product하고 더해버리면 해당 위치의 결과가 나오게 된다.
Parallel SpMV/CSR kernel
__global__ void SpMV_CSR(int num_rows, float* data, int* col_index, int* row_ptr, float* x, float* y) { int row = blockDim.x*blockIdx.x + threadIdx.x; if (row < num_rows) { float dot = 0; int row_start = row_ptr[row]; int row_end = row_ptr[row+1]; for (int i = row_start; i < row_end; i++) dot += data[i] * x[col_index[i]]; y[row] = dot; } }
CSR의 단점
첫 번째는 kernel의 memory access가 coalesce되지 않았다는 것이다.
위 예시로 보자면, 첫 번째 for문에서 thread 0은 data[0], thread 1은 x, thread 2는 data[2], thread 3은 data[5]에 접근한다. 다음 for문에서 thread 0은 data[1], thread 1은 x, thread 2는 data[3], thread 4는 data[6]에 접근한다. 때문에 memory coalesce가 발생하지 않는다.
두 번째는 divergence가 발생한다는 것이다.
각 thread가 수행하는 for문의 반복 회수는 해당 thread가 접근하는 row의 non-zero element의 개수인데, 이는 row마다 달라질 수 있기 때문에 반복 회수가 thread마다 매우 달라진다. 즉 divergence가 발생하게 된다.
Regularizing SpMV with ELL(PACK) Format : ELL

앞서 살펴본 CSR format의 divergence 문제와 memory access pattern 문제를 해결하기 위해 padding과 transpose를 적용해 해결할 수 있다.
먼저 non-zero element의 개수가 제일 많은 row를 찾는다. 이후 다른 row들은 해당 row와 크기가 동일하도록 padding(0)을 추가한다. 왼쪽 그림의 예시에서는 row 0에서는 1개, row 1에서는 3개, row 2에서는 0개, row 3에서는 1개의 padding이 추가된다. 이 때 col_index 배열 또한 같은 방식으로 padding을 적용해야 한다.
이 경우 몇몇 row만 다른 row들에 비해 훨씬 길면 padding이 비효율적으로 형성된다.
이후 이렇게 만들어진 data[]를 transpose한다. 이에 맞춰 col_index[]에 있는 값들도 mapping을 유지하기 위해 같은 방식으로 transpose한다.
그러면 row i의 시작이 위치가 data[i]로 바뀌었기 때문에 row_ptr이 필요없어진다.
ELL Kernel Design
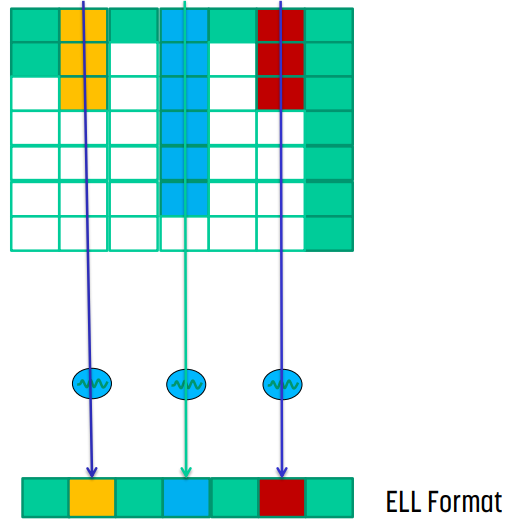

Parallel SpMV/ELL Kernel
__global__ void SpMV_ELL(int num_rows, float* data, int* col_index, int num_elem, float* x, float* y) { int row = blockDim.x*blockIdx.x + threadIdx.x; if (row < num_rows) { float dot = 0; for (int i = 0; i < num_elem; i++) dot += data[row + i*num_rows] * x[col_index[row + i*num_rows]]; y[row] += dot; } }
CSR과 비교하면 입력 parameter가 조금 달라진 것을 볼 수 있다. row_ptr이 사라지고 num_elem이 추가되었는데, 여기서 num_elem은 원래 matrix의 모든 row 중 non-zero element가 제일 많은 row의 element 개수이다.
padding을 추가했기 때문에 모든 row의 길이가 같아진다. 때문에 모든 thread들이 for문을 같은 회수만큼 반복하면 된다. padding의 경우 값이 0이기 때문에 결과에 영향을 미치지 않는다.
또한 for문 내에서 각 thread가 data[row + i*num_rows]에 접근하기 때문에 memory coalescing이 일어나므로 memory bandwidth를 더 효율적으로 사용할 수 있게 된다.
ELL format의 한계
예를 들어 1000 by 1000 size의 sparse matrix에서 1%의 element가 0이 아니라고 가정하자. 평균적으로는 각 row에는 10개의 non-zero element가 존재하게 되고, CSR format의 경우에는 사용하는 저장공간의 크기는 전체의 2% 정도이다.
그러나 row 중 하나가 non-zero element가 200고, 나머지는 매우 적은 경우, 모든 row에 size 200이 되도록 padding을 만들기 때문에 저장공간 압축 효율이 떨어진다.
즉, non-zero element가 많은 특별한 한 row가 있다면, CSR의 경우에는 하나의 warp만 오래 실행하지만, ELL은 모든 warp가 오래 실행된다.
또한 conversion에 대한 overhead도 존재한다. (큰 문제는 아니다)
ELLPACK variation

각 row에 non-zero element의 개수를 저장하는 방식이다.
Coordinate Format : COO

명시적으로 non-zero element에 대해 row/column index를 나열하는 방식이다.
이 경우, data[i]와 row_index[i]와 col_index[i]가 같이 움직이기만 한다면, 순서를 변경해도 정보가 유지되기 때문에 순서를 변경해도 된다.
Sequential SpMV/COO
data[i]의 element를 계산할 때는 y[row_index[i]] += data[i] * x[col_index[i]]만 실행해도 되고, 모든 data에 대해 이 연산을 수행하면 처리되는 순서에 상관없이 결과를 얻을 수 있다.
for (int i=0; i < num_elem; i++) { y[row_index[i]] += data[i] * x[col_index[i]]; }
COO Kernel Design
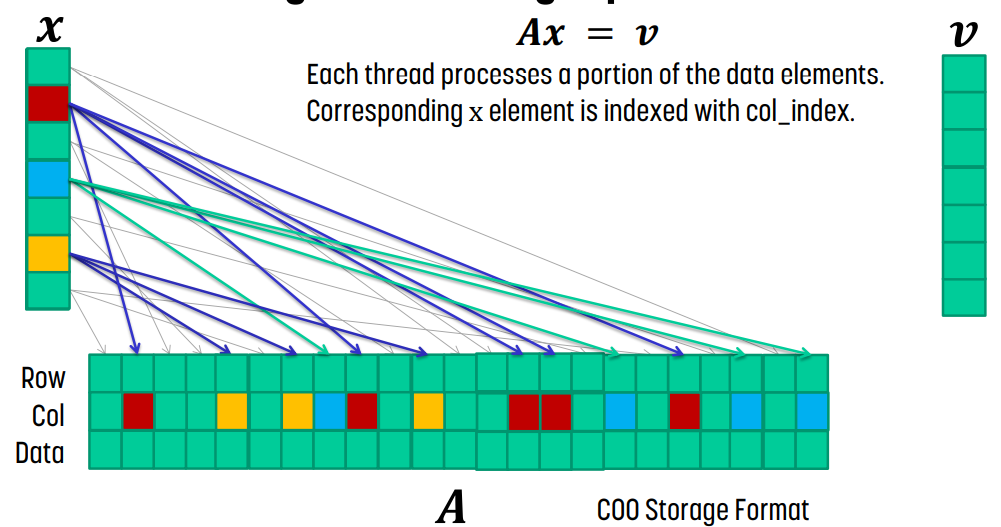
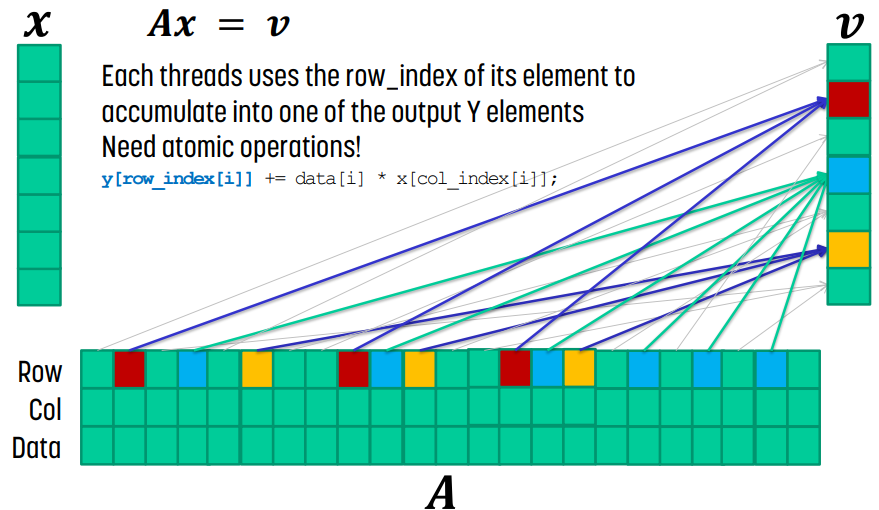
때문에 각 thread가 data의 특정 section을 담당하고 y[row_index[i]] += data[i] * x[col_index[i]] 연산을 수행한다. 이후 각 thread는 row_index[i]를 사용해서 output Y에 atomic operation을 사용해서 값을 누적하면 된다.
Parallel SpMV/COO Kernel
__global__ void SpMV_COO(float* data, int* col_index, int* row_index, int num_elem, float* x, float* y) { int i = blockDim.x*blockIdx.x + threadIdx.x; if (i < num_elem) { float dot = 0.0f; dot = data[i] * x[col_index[i]]; atomicAdd(&y[row_index[i]], dot); } }
design과 같은 방식으로 실행하면 된다.
Hybrid Format
ELL을 typical entry에 대해, COO를 exceptional entry에 대해 처리하는 방법이다. ELL을 적용할 때 non-zero element가 매우 많은 일부 row에 대해서만 COO를 적용하고 나머지를 ELL을 적용하는 것이다. 이를 통해 padding의 개수를 많이 줄일 수 있고, 나머지는 SpMV/COO를 사용해서 계산하는 방식이다.
예시
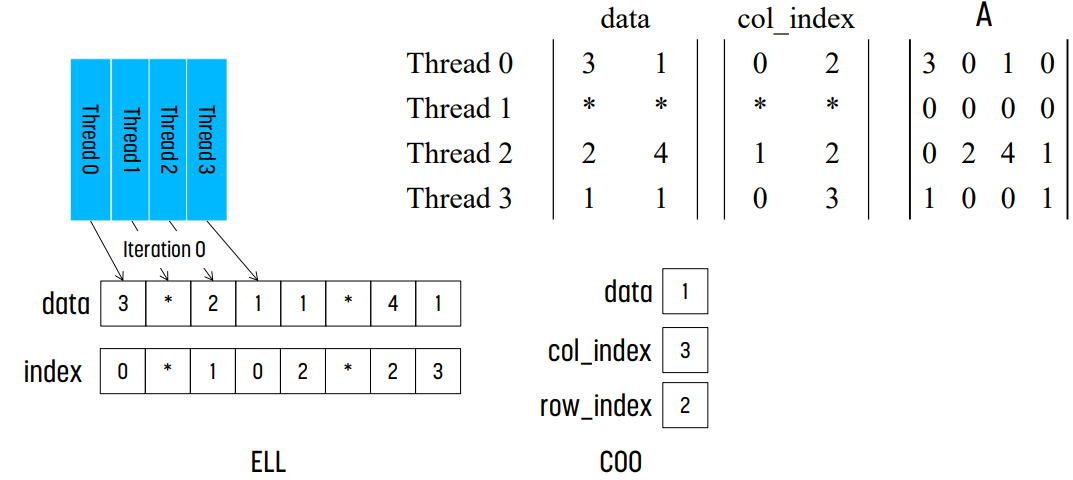
위 예시는 hybrid format의 예시를 보여준다.
[2, 3]에 해당하는 element 하나만 COO를 적용하고, 나머지를 ELL을 적용한 모습이다.
CSR Runtime
block performance는 non-zero element가 가장 많은 row에 depend한다.
Jagged Diagonal Sparse : JDS
load balancing을 위해 JDS를 구성한다.
JDS Kernel Design
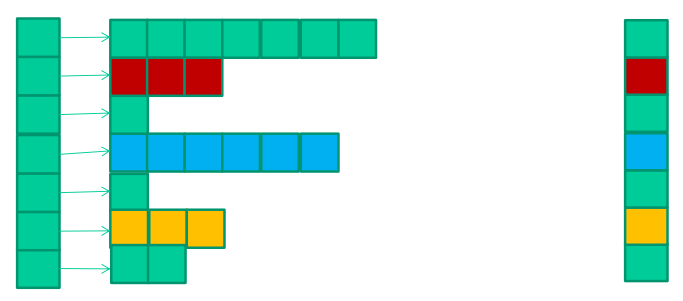

각 row의 non-zero element의 개수로 내림차순 정렬한다. 여기에 output vector를 올바르게 계산하기 위해 original row index를 추가로 가지고 있어야 한다.
예시
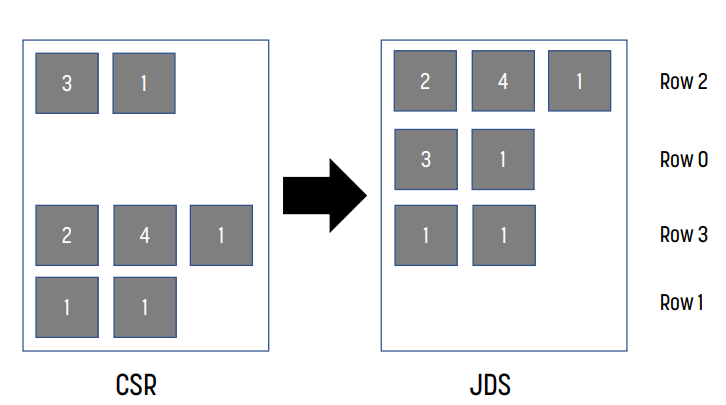
CSR to JDS conversion
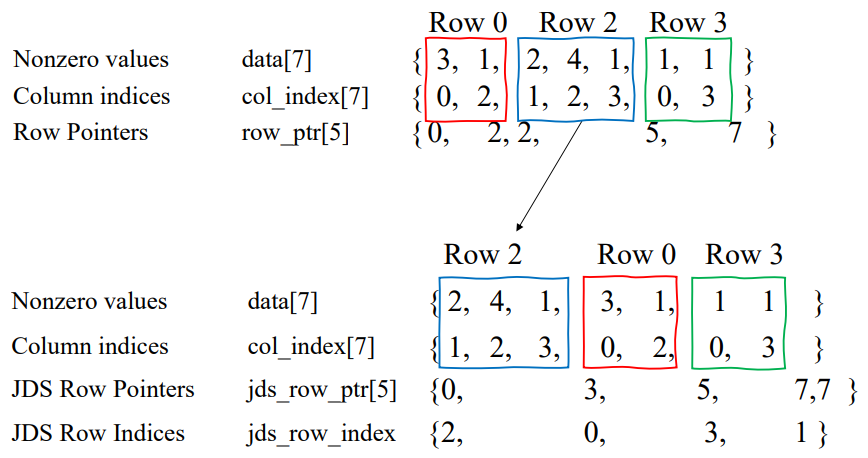

data[], col_index[]는 순서만 바뀌지만, row_ptr[]도 정렬 결과에 따라 바뀌어야 하고, original row index를 추가적으로 관리해 주어야 한다.
CSR과 같은 방식으로 해석하면 되지만, original row index를 나타내는 jds_row_index만 추가되었다고 보면 된다.
Parallel SpMV/JDS Kernel
__global__ void SpMV_JDS(int num_rows, float *data, int *col_index, int *jds_row_ptr, int jds_row_index, float *x, float *y) { int row = blockDim.x * blockIdx.x + threadIdx.x; if (row < num_rows) { float dot = 0; int row_start = jds_row_ptr[row]; int row_end = jds_row_ptr[row + 1]; for (int elem = row_start; elem < row_end; elem++) { dot += data[elem] * x[col_index[elem]]; } y[jds_row_index[row]] = dot; } }
CSR kernel과 대부분이 같지만, y[jds_row_index[row]] = dot 부분만 바뀌었다. original row index에 해당하는 위치에 값을 더해주어야 하기 때문이다.
JDS vs CSR control divergence
JDS kernel의 for문에서 thread는 여전히 iteration 회수가 다르다. 그러나 sort했기 때문에 인접한 thread들의 iteration 회수가 비슷하다. 때문에 CSR보다는 thread utilization이 좀 더 좋다.
JDS vs CSR memory divergence
그러나 여전히 memory coalesce가 발생하지 않는다는 문제가 있다.
JDS with Transposition
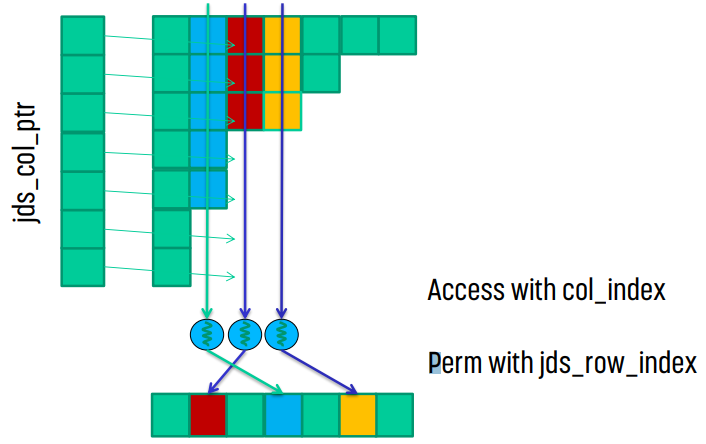
CSR 대신 ELL format을 적용했을 때를 생각해 보면, ELL은 transpose했기 때문에 memory coalesce를 할 수 있었다. 같은 방식으로 JDS도 transpose해서 memory coalesce를 노려볼 수 있을 것이다.
예시 : JDS transposition


transpose 이후 JDS format
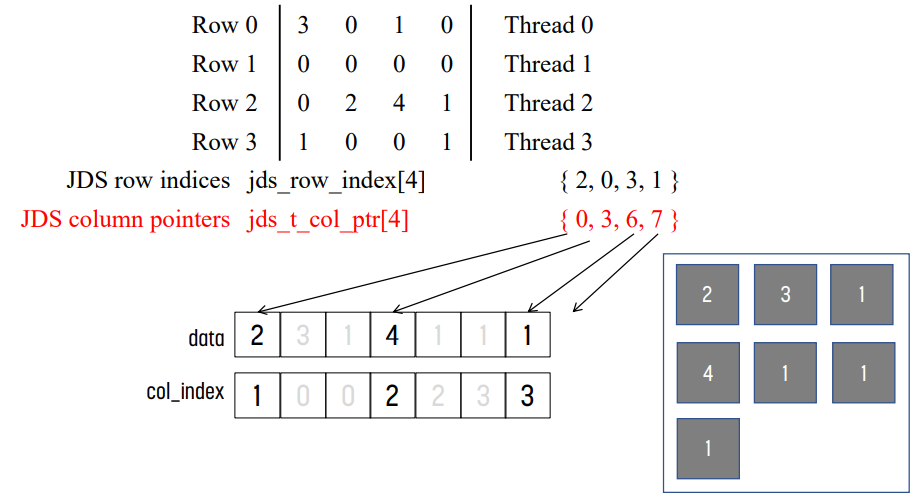
transpose하기 때문에 data[]와 col_index[]를 수정하고, jds_row_ptr 대신 jds_t_col_ptr를 사용해야 한다. jds_row_index는 original row index를 나타내는 것이므로 그대로 남겨둬야 할 것이다.
JDS : memory coalescing
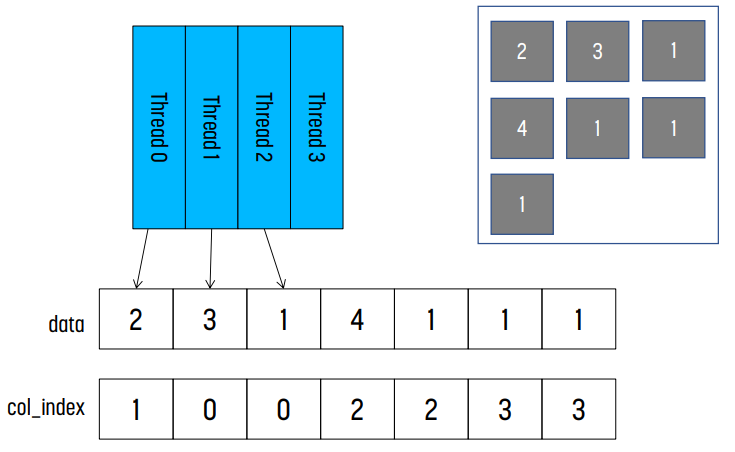

transpose하면 ELL과 같은 이유로 memory coalesce가 일어나기 때문에 더 효율적이게 된다.
언제 뭘 써야 할까?
무작위한 경우 : ELL
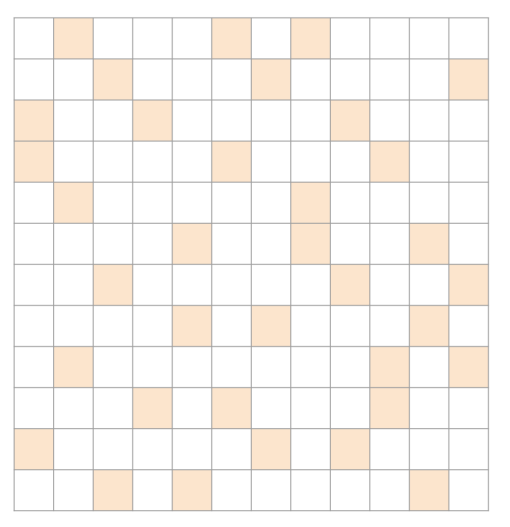
ELL이 제일 좋을 것이다. random하기 때문에 non-zero element도 균일하게 분포할 것이기 때문에 padding으로 인한 space overhead가 적을 것이다.
row의 편차가 큰 경우 : ELL/COO
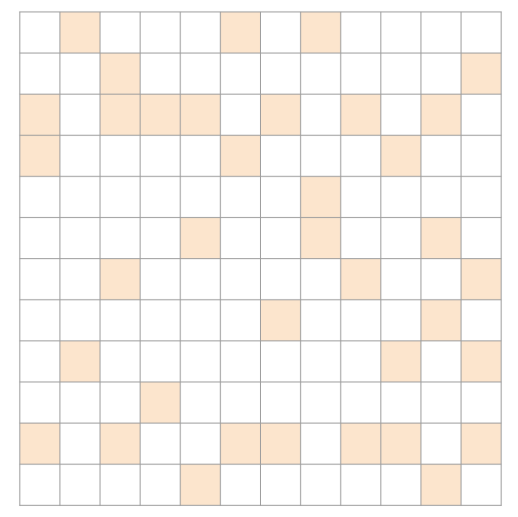
ELL/COO hybrid 방식이 제일 효율적일 것이다.
대부분 ELL 방식이 효율적이기 때문이다. 특히 긴 row들에 대해서는 COO로 처리하고, 나머지는 ELL 방식으로 처리하면 된다.
매우 sparse한 경우 : COO

COO가 제일 좋은 방식일 것이다. space overhead가 제일 적기 때문이다.
삼각형인 경우 : JDS
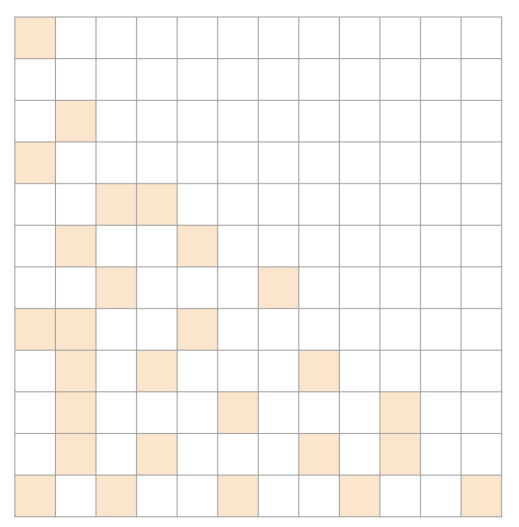
JDS가 제일 좋을 것이다. sparsity structure의 장점을 가져올 수 있기 때문이다.
banded matrix : ELL
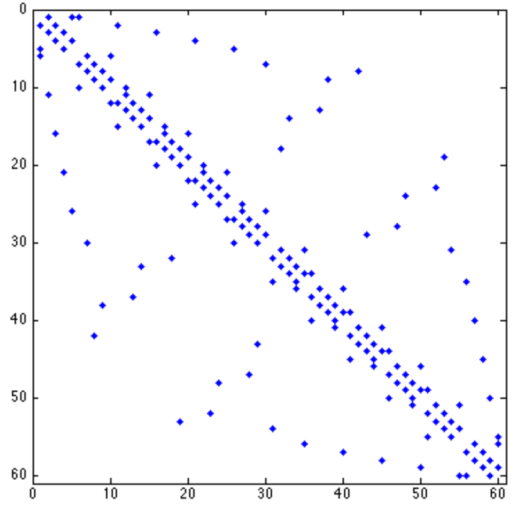
ELL이 제일 효율적일 것이다. 각 row의 편차가 적기 때문이다.
이외 다른 format들
- Diagonal(DIA) : strictly banded/diagonal인 경우 좋다.
- dense diagonal vector의 sparse set만 저장하고, 각 diagonal에 대해 main diagonal과의 offset을 저장하는 방식이다.
- Packet(PTK) : row/col 재배열로 diagonal submatrix 구성
- 인접한 row access가 인접한 element에 접근하기 때문에 cache performance가 좋다.
- Dictionary of Keys(DOK) : data의 row/col mapping 저장
- sparse matrix를 만들거나 query할 때 좋다.
- Compressed Sparse Column(CSC)
- Blocked CSR : block-sparse matrix에 유용하다.
- 이외, 이것들의 조합
Appendix: 고급 알고리즘을 위한 sparse matrix
- graph를 sparse adjacency matrix로 표현하기도 한다.
- binning technique(압축)는 data compaction을 위해 sparse matrix로 표현하기도 한다.
결론
- SpMV는 어렵다.
- 다른 표현 방식은 다른 storage requirement를 가진다.
- storage requirement는 sparsity pattern에 따라 다르다.
- regularity와 efficiency는 tradeoff가 있다.
- 몇몇 표현 방식은 제일 좋은 처리 방식이 있다.
- 높은 compute-to-communication ratio를 얻기 힘들다.
잘못된 내용이나 오탈자에 대한 지적, 질문 등은 언제나 환영합니다.
'CS > Parallel Computing' 카테고리의 다른 글
| [이종병렬컴퓨팅] Heterogeneous Parallel Computer를 위한 기술 스택 (0) | 2023.12.18 |
|---|---|
| [이종병렬컴퓨팅] OpenMP (0) | 2023.12.17 |
| [이종병렬컴퓨팅] Parallel Patterns : Scan (0) | 2023.12.17 |
| [이종병렬컴퓨팅] Parallel Patterns : Reduction (0) | 2023.12.16 |
| [이종병렬컴퓨팅] Parallel Patterns : Histogram (0) | 2023.12.16 |
- Sparse Matrix
- Sparse Matrix Format
- 간단한 Parallel SpMV
- Compressed Sparse Row Format : CSR
- Parallel SpMV/CSR kernel
- CSR의 단점
- Regularizing SpMV with ELL(PACK) Format : ELL
- Parallel SpMV/ELL Kernel
- ELL format의 한계
- Coordinate Format : COO
- Parallel SpMV/COO Kernel
- Hybrid Format
- Jagged Diagonal Sparse : JDS
- Parallel SpMV/JDS Kernel
- JDS vs CSR control divergence
- JDS vs CSR memory divergence
- JDS with Transposition
- 언제 뭘 써야 할까?
- 결론
![[이종병렬컴퓨팅] Parallel Patterns : Sparse Computation](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FdKTUya%2FbtsB80IyVwl%2Fiph60GEykxceENex8zohHk%2Fimg.png)