이 글은 RWTH AACHEN 대학교 Joost-Pieter Katoen 교수님의 2018년 1학기 Introduction to Model Checking 강의와 Principles of Model Checking을 기반으로 재구성한 것입니다.
이 글에서는 model checking에서 사용하는 transition system이 대체 뭔지, 그리고 우리가 사용하는 일반적인 프로그램을 transition system으로 바꾸는 방법을 살펴본다.
Transition System
transition system은 directed graph로 나타낸다. 이 때 graph의 node는 state를, edge는 transition을 의미한다.
Definition. Transition System
transition system TS는 (S, Act, → I, AP, L)의 tuple로 표기한다.
- `S`는 state의 집합
- `Act`는 action의 집합
- `→`는 S × Act × S의 부분집합이며, transition relation을 의미한다.
- 편의상 (s, $\alpha$, s') ∈ → 대신
- s$\overset{\alpha}{\rightarrow}$s'으로 표기한다.
- 이 때 s ∈ S, s' ∈ S이고 $\alpha$ ∈ Act이다.
- state s에서 action $\alpha$를 통해 s'로 transit된다고 이해하면 될 것 같다.
- `S$_0$` ⊆ S이며, 초기 state를 의미한다.
- S$_0$의 원소가 하나인 경우는 거기서 시작하지만, 2개 이상인 경우에는 non-deterministic하게 시작 위치가 결정된다. 정말 간단하게 말하자면 random하게 고른다는 뜻이다.
- `AP`는 Atomic Propisition들의 집합으로, state의 property를 의미한다.
- `L`은 S → $2^{\text{AP}}$, labeling function을 의미한다. 모든 state을 AP의 power set에 매핑하는 것이다.
- state와 property의 매핑이라고 이해하면 된다.
- L(s) = ap라고 하면, state s의 property가 ap라는 뜻이다.
- state와 property의 매핑이라고 이해하면 된다.
이 때 TS는 S, Act, AP가 finite면 finite이다.
Transition System 예시
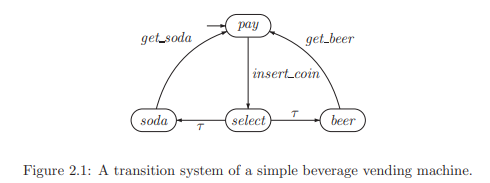
이런 transition system이 있을 때, 다음과 같이 표기할 수 있다.
- S = {pay, select, soda, beer}
- Act = {get_soda, get_beer, insert_coin, $\tau$}
- →는 위 그림의 모든 edge.
- S$_0$ = {pay}
- AP와 L은 property를 어떻게 설정하냐에 따라 달라진다.
- "vending machine이 코인을 넣은 후에만 음료를 준다"라는 property를 택한다고 하자.
- 그러면 AP = {pay, drink}로 설정할 수 있고, 이 경우 L(pay) = {pay}, L(soda) = L(beer) = {paid, drink}, L(select) = {paid}로 둘 수 있다.
Definition. Predecessors and Successors
직역하면 전임자와 후임자이다. s ∈ S 그리고 $\alpha$ ∈ Act일 때,
- s의 $\alpha$-successors는 다음와 같이 정의한다.
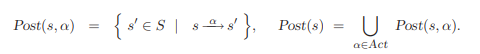
어떤 state s에서 action alpha를 통해 s'로 갈 수 있을 때, Post(s, $\alpha$) = s'들의 집합이다. Post(s)는 모든 $\alpha$에 대해 Post(s, $\alpha$)의 합집합이다.
graph식 언어로 표기하면, Post(s, $\alpha$)는 state s에서 edge $\alpha$를 통해 갈 수 있는 neighbor들은, Post(s)는 $state s의 모든 neighbor를 말하는 것이다. 이렇게 생각하면 predecessors도 바로 이해할 수 있다.
- s의 $\alpha$-predecessors는 다음과 같이 정의한다.
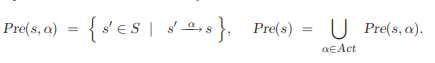
어떤 state s'에서 alpha를 통해 s로 갈 수 있을 때 Pre(s', $\alpha$) = s일 때 s'의 집합이다. Pre(s)는 모든 $\alpha$에 대해 Pre(s, $\alpha$)의 합집합이다.
Definition. Terminal State
transition system의 state s에 대해 Post(s) = $\phi$일 때 s를 terminal state이라고 한다.
graph식 언어로 표기하자면 outgoing edge가 없는 node를 terminal로 말한다는 것이다.
parallel system을 모델링할 때 terminal state는 바람직하지 않은 것으로 간주한다.
Definition. Execution Fragment
finite exeucution fragment는 다음과 같이 정의한다. 이 때 n $\ge$ 0일 때 n을 execution fragment length라고 한다.

infinite execution fragment는 다음과 같이 정의한다.

infinite execution fragment의 odd-length prefix는 finite execution fragment이다. `??? 여기 잘 모르겠음`
graph식 언어로 표기하자면 path라고 생각하면 된다.
Definition. Maximal & Initial Execution Fragment
finite execution fragment가 terminal state로 종료되거나, infinite execution fragment인 경우 이들을 maximal execution fragment라고 한다.
execution fragment가 initial state에서 시작하는 경우 initial execution fragment라고 한다.
Definition. Transition System Exeuction
transition system TS의 execution은 initial & maximal execution fragment다. 즉, initial state에서 시작해야 하며, terminal state로 종료되거나 또는 infinite execution fragment여야 한다.
Definition. Reachable States
transition system TS의 execution이 있을 때, 다음과 같은 initial, finite execution fragment에 대해 아래 조건을 만족하는 s를 reachable이라고 한다.
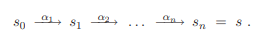
앞서 설명했듯 TS의 execution은 initial & maximal execution fragment이므로 s$_0$ ∈ S$_0$이다.
graph식으로 설명하면, initial node에서 어떤 edge를 거쳐 해당 node까지 도달할 수 있다면 해당 node를 reachable이라고 한다.
Reach(TS)는 TS의 모든 reachable state를 의미한다.
여기까지 Transition System에 대해 살펴봤다. model checking에서 우리가 하고자 하는 것은 어떤 system을 modeling한 transition system TS와, requirement를 model checker에 넣어 OK인지 NO인지 얻어내는 것이다. 지금까지 TS를 살펴봤다.
HW/SW modeling
46p 참고.
HW modeling은 transition system을 modeling하는 것과 같다. state를 정의하고, initial state를 정의하고, state에 따라 next input으로 인해 다음 state가 정해지므로, 이를 기반으로 →를 얻을 수 있다. 이후 AP와 L은 어떻게 설정하느냐에 따라 달라진다.
Data Dependent System
Data Dependent System은 conditional branch에 의존하는 system을 의미한다. Data Dependent System을 transition system으로 모델링할 때는 conditional transition을 사용하며, condition으로 label을 지정하는 resulting graph를 사용한다.
단편적으로만 살펴보면, conditional branch로 나타낸 program graph는 다음과 같은 과정을 통해 transition system으로 변환할 수 있다.
- 이를 위해 첫째로 program counter에 대해 알아야 하고, 둘째로 관련된 모든 데이터(모든 변수들)를 알아야 한다. 이 2가지를 합쳐 transition system의 state로 표현하고, 조건에 따라 다음 state로 transit하게 만들면 된다.
- program counter의 각 assignment에 해당하는 명령어를 action으로 만든다. 그러면 transition relation이 만들어진다.
일단은 Data Dependent System을 Program Graph로 나타내고, 이를 Transition System으로 변환하는 방법을 살펴보겠다. 그 전에 program graph에서 사용하는 몇 가지 개념부터 살펴보겠다.
Definition. Evaluation function
먼저 typed variable는 variable x와 x의 domain Dom(x)로 이루어진다.
- boolean의 경우 Dom(x) = {0, 1}
- integer의 경우 Dom(x) = N(정수)
- 와 같이, domain은 해당 변수가 가질 수 있는 값들의 집합이다.
Dom(x)가 0, 1인 boolean variable인 경우 Value는 0, 또는 1을 가지고 있게 된다.
이 변수를 formalize하기 위해 evaluation function $\eta$를 두어 변수를 evaluate한다.
코딩하면서 변수에 값을 넣는다는 개념이 아니라, 변수에 있는 값을 꺼내오는 함수를 만든 것이라고 생각하면 된다.
Var를 typed variable들의 집합, Values를 $\bigcup_{x \in Var}^{} Dom(x)$(Var에 있는 모든 변수들의 domain의 합집합)이라고 할 때, evaluation function $\eta$는 Var에서 Values를 매핑하는 함수이다. 이 때 $\eta$는 type consistent하기 때문에 해당 변수의 type을 유지한 채로 값을 꺼내온다. 즉, x ∈ Var인 x에 대해 $\eta$(x) ∈ Dom(x)가 된다는 것이다.
Eval(Var)는 Var의 evaluation function들의 집합이라 정의한다.
Definition. Conditions of Typed Variables - Guard
앞서 Var를 typed variable들의 집합이라고 했다. Cond(Var)는 Var에 있는 변수들의 boolean condition을 의미한다. 이를 guard라고 부르기도 한다.
¬x ∧ y < z와 같은 예시들이 있다.
Definition. Satisfaction Relation
앞에서 Var, Eval(Var), Cond(Var)를 정의했다. 이들을 사용해서 조건을 만족하는지 여부를 수식으로 표현할 수 있다.
- Eval(Var)가 Cond(Var)를 만족하는 경우 Eval(Var) $\models$ Cond(Var)로 표기한다.
- Eval(Var)가 Cond(Var)를 만족하지 않는 경우 Eval(Var) $\not\models$ Cond(Var)로 표기한다.
아래와 같은 예시들이 있다.
|x = 0, y = 3, z = 6| $\models$ ¬x ∧ y < z
|x = 0, y = 3, z = 6| $\not\models$ x ∨ y = z
Definition. Effect function
effect function은 다음 매핑을 의미한다: Effect : Act × Eval(Var) → Eval(Var)
앞서 설명했든 모든 변수들에 있는 값들은 변수와 값을 매핑하는 함수인 Eval()에 의해 결정된다. 즉, 위 수식이 의미하는 것은 기존 변수들의 값에 Act(실행해야 하는 코드, assignment에 해당하는 코드)으로 계산한 새로운 변수들의 값이다.
$\alpha$가 action(assignment에 해당하는 코드), $\eta$가 evaluation function일 때 표기는 Effect($\alpha$, $\eta$)와 같이 한다.
$\alpha$가 x = 2x + y;인 경우
Effect($alpha$, [x = 1, y = 3]) = [x = 5, y = 3]
$\alpha$가 x = 2x + y; y = 1-x인 경우
Effect($alpha$, [x = 1, y = 3]) = [x = 5, y = -4]
Definition. Program Graph
program graph PG는 (Loc, Act, Effect, →, Loc$_0$, g$_0$)으로 표기한다.
- `Loc`은 location의 (finite) 집합. 각 program graph의 node라고 생각하면 된다.
- program의 line은 finite하기 때문이다.
- `Act`는 action의 집합
- `Effect`는 Act × Eval(Var) → Eval(val)이며, 현재 값으로 다음 값을 계산하는 함수이다.
- `→`는 Loc × Cond(Var) × Act × Loc이며, conditional transition relation을 의미한다.
- 편의상 → 대신 $\text{l} \overset{g:\alpha}{\rightarrow} \text{l'}$으로 표기하며, l ∈ Loc, l' ∈ Loc, g ∈ Cond(Var), $\alpha$ ∈ Act이다.
- (l, g, $\alpha$, l')으로 표기하기도 한다.
- location l에서 g를 만족할 때 $\alpha$를 수행해 l'로 가는 transition을 의미한다.
- `Loc$_0$` ⊆ Loc은 initial location을 의미한다.
- `g$_0$` ∈ Cond(Var)는 initial condition을 의미한다.
Program Graph → Transition System으로 변환
Var을 사용하는 Program Graph의 동작은 아래와 같은 로직을 따라 Transition System Sementics로 바꿀 수 있다.

- state는 2가지를 포함한다: program counter(location)과 variable evaluation이 그것이다. <l, $\eta$>로 표현하며 l은 location을, $\eta$는 variable을 값으로 매핑하는 함수인 variable evaluation function을 의미한다.
- state는 location과 evaluation의 쌍으로 이뤄져 있다!
- 때문에 S = Loc × Eval(Var)이다. 이 중 도달 불가능한 state도 있겠지만 가능한 모든 경우를 취한다.
- S$_0$는 {<l, $\eta$> : l ∈ Loc$_0$, $\eta \models g_0$}로 포현한다.
- 초기 location 중 가능한 모든 값과, g$_0$(초기 Cond(Var)) 중 가능한 모든 값들의 cartesian production이다.
- → (transition relation)
- 분모의 좌항은 Program Graph의 →에 해당하는 항으로 conditional transition relation을 의미한다. 여기에서 g를 만족하는 $\eta$만 이 conditional transition을 사용할 수 있기 때문에 g와 and 연산을 취한다.
- 즉, g를 만족하는 변수값들만 해당 conditional transition relation을 탈 수 있다는 말이다.
- 분자 부분은 한 state <l, $\eta$>에서 action $\alpha$를 사용해 <l', Effect($\alpha, \eta$)>로 간다는 것을 의미한다.
- 이 분수가 의미하는 것은, [분자 부분의 조건이 만족하면 분모 부분의 조건도 만족한다]는 것이다.
- 이 때 Transition System의 transition relation은 해당 분수식, 즉 다음 식을 만족하는 제일 작은 relation이다. - if $\text{l} \overset{g:\alpha}{\rightarrow} \text{l;}$ ∧ $\eta \models$ g then <l, $\eta$> $\overset{\alpha}{\rightarrow}$ <l', Effect($\alpha, \eta$)>
- 분모의 좌항은 Program Graph의 →에 해당하는 항으로 conditional transition relation을 의미한다. 여기에서 g를 만족하는 $\eta$만 이 conditional transition을 사용할 수 있기 때문에 g와 and 연산을 취한다.
- AP는 Loc ∪ Cond(Var)이다.
- labeling function은 location l과모든 Cond(Var)를 만족하는 현재의 evaluation $\eta$들의 합집합이다.
위 방법을 사용해 모든 Program Graph를 Transition System으로 바꿀 수 있다. 이 때 evaluation function에서 정수와 같은 무한한 집합을 사용하기 때문에 - Eval(Var)가 무한하기 때문에 state set S도 무한하다. 즉 이렇게 변환한 transition system은 infinite state를 가진다.
'Project > Model Checking' 카테고리의 다른 글
| [Maude] Token Ring 검증 (0) | 2023.10.23 |
|---|---|
| [Model Checking] Designing Reliable Distributed Systems (0) | 2023.10.09 |
| [Model Checking] 과제연구 주제 정리 (0) | 2023.09.19 |
| [Model Checking] Linear Time Properties (0) | 2023.09.19 |
| [Model Checking] Modeling Concurrent System (0) | 2023.09.13 |
![[Model Checking] Transition System과 Program Graph](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbdPktf%2FbtstwHrZysv%2FhoRUI4TpZMaoi706Kf030k%2Fimg.png)