이 글은 RWTH AACHEN 대학교 Joost-Pieter Katoen 교수님의 2018년 1학기 Introduction to Model Checking 강의와 Principles of Model Checking을 기반으로 재구성한 것입니다.
지난 글에서는 Transition System과 Program Graph, 그리고 Program Graph를 Transition System으로 변환하는 방법을 살펴 봤다. 여기서 살폈었던 것들은 닫힌 계로써, 단 하나의 프로그램만 모델링하는 방법이었다.
이제 총 n개의 parallel system P$_1$, P$_2$, ... P$_n$ 이 있을 때를 모델링하고자 한다. 이 때 각 thread의 행동은 아래 3가지 중 하나이다.
- no communication (interleaving) : system이 `independent`할 때 (서로 communication하지 않을 때)
- synchronous communication (handshaking) : system들이 `shared variable`를 사용해 communication을 할 때
- asynchronous communication (channel) : `queue`를 사용해 communication할 때
이 글에서는 위 3가지를 어떻게 transition system으로 표현하는지 살펴볼 것이다.
Interleaving
interleaving communication은 parallel process들의 concurrent, independent action을 의미한다. (서로 communication하지 않는다.) 때문에 interleaving(끼워넣기)라고 표현한다. 앞서 그랬듯 이 process들은 nondeterministic하게 다음 action을 결정한다. 기호로는 `|||`로 표기한다.
interleaving에서 중요한 점은 action $\alpha$와 $\beta$가 어떤 순서로 실행되든 결과가 같다는 것이다. 이를Effect($\alpha$ ||| $\beta$) = Effect($(\alpha; \beta)$ + $(\beta; \alpha)$)로 표현한다.
Definition. Transition System의 Interleaving
transition system TS$_1$이 (S$_1$, Act$_1$, →$_1$, I$_1$, AP$_1$, L$_1$), TS$_2$ (S$_2$, Act$_2$, →$_2$, I$_2$, AP$_2$, L$_2$)일 때 이 둘의 interleaving 결과 TS$_1$ ||| TS$_2$는 다음과 같이 정의한다.

- interleaving system의 state들은 각 transition system의 state들의 cartesian product가 될 것이다.
- →는 $\frac{s_1 \overset{\alpha}{\rightarrow} s'_1}{<s_1, s_2> \overset{\alpha}{\rightarrow} <s'_1, s_2>}$ AND $\frac{s_2 \overset{\alpha}{\rightarrow} s'_2}{<s_1, s_2> \overset{\alpha}{\rightarrow} <s_1, s'_2>}$로 정의한다.
- 좌항의 분자가 의미하는 것은 $s_1$에서 $\alpha$를 통해 $s'_1$으로 이동하는 TS$_1$의 transition relation을 의미한다. 분모가 의미하는 것은 state <$s_1$, $s_2$>에 대해 $\alpha$를 통해 <$s'_1$, $s_2$>로 이동하는 transition relaction을 의미한다. 이 때 TS$_2$의 transition은 일어나지 않는다!
- 우항도 똑같은 방식으로 이해할 수 있다.
- 이전에 살펴봤듯 이 분수식이 의미하는 것은 [분자 부분이 참이면 분모 부분을 만족하는데, 이 중 제일 작은 relation]이다.
- L(s$_1$, s$_2$) = L(s$_1$) ∪ L(s$_2$)로 정의한다.
interleaving의 경우 서로 영향을 주지 않기 때문에 cartesian produce와 union으로 표현된다.
Communication via Shared Variables
interleaving의 경우에는 공유하는 변수가 없어 두 subsystem의 cartesian product를 하면 되었다. 그러나 만약 어떤 variable이 shared variable인 경우에는 어떻게 될까?
예를 들어 어떤 shared variable x를 사용하는 transition system 1, transition system 2가 있다고 하자. 둘의 interleaving 결과로 <x=4, x=6>와 같은 존재할 수 없는, inconsistent state가 생성된다. 이를 해결하기 위해 shared variable을 사용하는 경우는 따로 정의해 주어야 한다.
shared variable을 사용하는 parallel program의 transition system을 바로 합치는 것은 어렵기 때문에 program graph 단계에서 interleaving을 통해 shared variable을 먼저 정의하고, 이후 합친 program graph를 transition system으로 전환해 shared variable을 사용하는 transition system을 정의한다.
Definition. Program Graph의 Interleaving
program graph PG1와 program graph PG2의 interleaving은 다음과 같다. (단순한 cartesian product이다.)
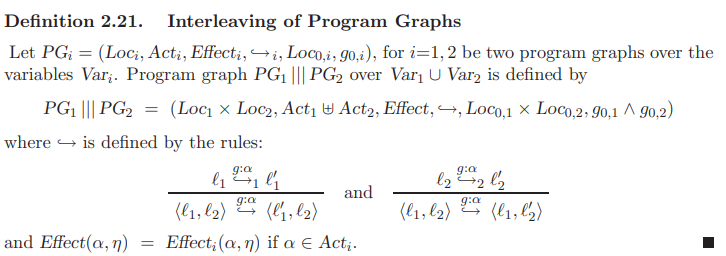
- Loc의 경우 Loc$_1$과 Loc$_2$의 cartesian product이다.
- →는 위 그림과 같이 정의한다.
- program grpah의 edge에는 guard와 action이 있었다.
- 좌항의 분자 $\text{l} \overset{g:\alpha}{\rightarrow} \text{l'}$는 location l에서 g를 만족할 때 $\alpha$를 수행해 l'로 가는 transition을 의미한다.
- 좌항의 분모는 location <l$_1$, l$_2$>에서 g를 만족할 때 $\alpha$를 수행해 <l'$_1$, l$_2$>로 transition 할 수 있다는 것이다.
- 이 분수식이 의미하는 것은 [분자 부분이 참이면 분모 부분도 참인데, 이를 만족하는 relation 중 제일 작은 relation]이다.
- 우항도 같은 방식으로 이해할 수 있다.
- L(s$_1$, s$_2$) = L(s$_1$) ∪ L(s$_2$)로 정의한다.
- guard는 각각의 guard의 or 연산이다.
- shared varibale는 Var1 ∩ Var2이고, Var1 ∪ Var2 - (Var1 ∩ Var2)가 local variable이 된다.
program graph는 shared variable을 허용하는데, program graph에서는 state에 변수의 값이 들어가지 않고 location이 들어가기 때문이다.(변수의 값을 얻기 위해서는 evaluation function을 사용해야 한다.) 이후 이를 transition system으로 변환할 때, location과 evaluation을 state로 만드는 특성 때문에 program graph의 interleaving을 transition system으로 전환하면 shared variable을 사용할 수 있게 된다.
이 때문에 다음 특성이 성립한다.
PG = PG$_1$ ||| PG$_2$, TS$_1$ = TS(PG$_1$), TS$_2$ = TS(PG$_2$)라고 정의했을 때
shared variable이 없는 경우에는 TS$_1$ ||| TS$_2$ = TS(PG)이지만
shared variable이 있는 경우에는 TS$_1$ ||| TS$_2$ ≠ TS(PG)이다.
Mutual Exclution with Semaphore
semaphore와 같이 shared variable을 사용해서 mutual exclusion을 구현하는 경우를 생각해 보자. (42p 참고) 글로 다 나와있는 내용이라 세부 내용은 생략하지만 중요한 부분만 기술하면 아래와 같다.
- PG 2개를 interleaving한 후, 만들어진 location들 중에서 reachability를 따진다.
- reachable한 state들만 따져서 transition system으로 바꾼다.
- critical section으로 둘 다 들어갈 수 있는지 / 둘 다 wait하는 상태는 없는지 확인한다.
Perterson's Mutual Exclution Algorithm
45p 참고
Synchronous Message Passing (Handshaking)
synchronous message passing (handshaking)이란 interacting하는 transition system들이 synchronous하게 특정 action을 처리해야 한다는 것을 의미한다. 즉, 2개 이상의 transition system이 동시에 특정 action을 수행해야 한다는 것이다.
이를 위해 새로운 operator ||$_{H}$를 정의한다. 이 연산자는 independent action에 대해서는 interleaving하고, H에 있는 action들에 대해서는 synchronization action을 취하는 연산을 의미한다.

- S, Act, →, I, AP, L에 대해서 모두 cartesian product를 적용한다.
- →는 아래와 같이 이다. 요약하자면 즉 H에 있지 않은 $\alpha$에 대해서만 기존 relation을 가져오고, H에 있는 것들은 새로 정의한다.
- $\alpha$ ∈ Act$_i$ \ H인 $\alpha$에 대해서 : $\frac{s_1 \overset{\alpha}{\rightarrow} s'_1}{<s_1, s_2> \overset{\alpha}{\rightarrow} <s'_1, s_2>}$ AND $\frac{s_2 \overset{\alpha}{\rightarrow} s'_2}{<s_1, s_2> \overset{\alpha}{\rightarrow} <s_1, s'_2>}$로 정의한다.
- 위의 interleaving과 같다.
- $\alpha$ ∈H인 $\alpha$에 대해서 : $\frac{s_1 \overset{\alpha}{\rightarrow} s'_1 \cap s_2 \overset{\alpha}{\rightarrow} s'_2}{<s_1, s_2> \overset{\alpha}{\rightarrow} <s'_1, s'_2>}$로 정의한다.
- 이는 s$_1$에서 $\alpha$를 수행해 s'$_1$으로 가고, s$_2$에서 $\alpha$를 수행해 s'$_2$으로 가고, 이 때 state는 <s$_1$, s$_2$>에서 <s'$_1$, s'$_2$>로 가는 relation 중 제일 작은 것을 의미한다.
- $\alpha$ ∈ Act$_i$ \ H인 $\alpha$에 대해서 : $\frac{s_1 \overset{\alpha}{\rightarrow} s'_1}{<s_1, s_2> \overset{\alpha}{\rightarrow} <s'_1, s_2>}$ AND $\frac{s_2 \overset{\alpha}{\rightarrow} s'_2}{<s_1, s_2> \overset{\alpha}{\rightarrow} <s_1, s'_2>}$로 정의한다.
Properties of Handshaking
transition system들의 handshaking은 commutative(교환 가능)하지만 not associative(결합 불가능)이다. 단, 모든 transition system이 같은 H에 대해 synchronize하는 경우에는 associative이다.
이 때 H = Act$_1$ ∩ Act$_2$일 때는 H를 생략하고 ||로 표기한다.
또한 H = $\phi$인 경우에는 interleaving operator로 표기할 수 있다. (TS$_1$ ||$_{\phi}$ TS$_2$) = TS$_1$ ||| TS$_2$)
예시

왼쪽과 같은 transition system TS$_1$, TS$_2$가 있을 때 TS$_1$ ||$_{\beta}$ TS$_2$는 오른쪽 그림과 같다. $\beta$를 수행하기 전 state까지 기다리고, 이후에 $\beta$를 수행한다.
Synchronous Message Passing using Arbiter
arbiter는 2개의 state가 있는 machine이다. 두 transition system과 arbiter가 synchronize되므로, arbiter의 action을 통해서만 lock을 얻을 수 있다는 것이 핵심이다.
만약 두 transition system 모두 wait 상태라면, arbiter는 둘 중 하나만 non-deterministic하게 request 상태로 바꿔줄 수 있다. (arbiter의 resource가 한정되어 있기 때문이다.)
이를 식으로 표현하면 TS$_{\text{Arb}}$ = (TS$_1$ ||| TS$_2$) || Arbiter이다. TS$_1$과 TS$_2$는 서로 communication하지 않기 때문에 interleaving으로, 이 둘의 interleaving 결과와 arbiter가 synchronize한다는 것을 의미한다.
Channel System
data-dependent parallel system은 아래의 3가지로 표현한다.
- shared variable들로 communication
- synchronous message passing (handshaking)
- asynchronous message passing
한편, channel system은 FIFO 형태의 buffer인 channel로 통신하는 parallel system이다. 이 때 buffer size가 0이면 synchronous message passing, 즉 handshaking을 의미하고 buffer size가 0보다 크면 delay가 있는 asynchronous pessage passing을 의미한다.
앞서 handshaking은 살펴봤으니 여기서는 asynchronous message passing을 살펴볼 것이다.
Asynchronous Message Passing
synchronous handshaking에서는 동기화된 action들은 동시에 실행되어야 했다. 반면 asynchronous의 경우 sender가 channel에 message를 보내면, receiver는 그 message를 (여유가 있을 때) 확인한다.
이를 위해 sender, receiver 2개의 program graph, 그리고 buffer를 정의해야 한다. 참고로, channel system은 program graph를 사용해 정의한다.
Definition. Communication Action
buffer에 대한 action인 communication action 2가지를 새로 정의하자. 참고로, 이 둘의 합집합을 Comm이라고 부르기도 한다.
- c!v : value v를 channel c에 넣는다.
- c?x : channel c에서 message를 받아 variable x에 넣는다.
cap(c) > 0일 때 c!v와 c?x의 동작은 다음과 같다.
- c!v : c의 capacity가 가득 차지 않았을 때만 가능하다. 하는 동작은 enqueue(c, v)이다.
- c?x : c가 비지 않았을 때만 가능하다. 하는 동작은 <x := front(c); dequeue(c)>이다.
- 조건을 만족하지 않는 동작은 정의하기에 따라 다르다.
그럼 기존에는 어떤 action $\alpha$에 대해 $\text{l} \overset{g:\alpha}{\rightarrow} \text{l'}$로 정의했던 것에 communication action도 추가할 수 있다. 추가하는 action들은 다음과 같다.
$\text{l} \overset{g:c!v}{\rightarrow} \text{l'}$와 $\text{l} \overset{g:c?x}{\rightarrow} \text{l'}$
- $\text{l} \overset{g:c!v}{\rightarrow} \text{l'}$는 location l에서 g가 true일 때 value v를 channel에 넣는 것을 통해 l'로 가는 것을 의미한다.
- $\text{l} \overset{g:c?x}{\rightarrow} \text{l'}$는 locaiton l에서 g가 true일 때 channel에서 message를 받아 variable x에 넣는 것을 의미한다.
- 이 때 channel에서 message를 받을 때는 front()에 있는 것을 가져온다.
Definition. Channel
이전 포스트에서 typed variable x의 domain을 Dom(x)라고 했고, 모든 x에 대해 모든 Dom(x)들의 합집합을 Var로 정의했고, $\eta$를 Var과 Values를 매핑하는 evaluation function으로 정의했었다.
channel 이와 유사하게 정의할 것이다.
typed channel c를 다음과 같이 정의한다: typed channel c에 대해 capacity cap(c) ∈ {0, 자연수} ∪ {∞}이고 domain Dom(c)를 가진다.
- 뜻은 capacity가 0과 자연수 또는 unbounded이고, 들어갈 수 있는 값이 Dom(c)라는 뜻이다.
Definition. Channel Evaluation Function
typed channel에 대한 evaluation function $\xi$는 Chan과 Values*를 매핑하는 함수이며, $\xi$(c)는 Dom(c)에 속하고, 길이가 cap(c)보다 작거나 같아야 한다고 정의한다. 이 때 Chan은 typed channel의 합집합을, Values*는 channel 안에 담긴 finite한 값을 의미한다. 따라서
Definition. Channel System
communication action, channel, channel evaluation function을 정의했으므로 이제 channel system를 정의해 보자.
channel system은 P$_i$를 (Var, Chan)에 대한 program graph라고 두었을 때 [ P$_1$ | P$_2$ | ... | P$_n$ ]라고 정의한다.
- Var는 typed variable의 set을, Chan은 typed channel의 set을 의미한다.
이 때 (Var, Chan)에 대한 program graph P$_i$는 (Loc$_i$, Act$_i$, Effect$_i$, →$_i$, Loc$_{0,i}$, g$_i$)로 표기하며, channel에 대한 정보만 추가하기 위해 →만 새로 정의한다. 나머지는 앞서 살펴봤던 program graph P$_i$의 정의 (Loc$_i$, Act$_i$, Effect$_i$, →$_i$, Loc$_{0,i}$, g$_i$)와 동일하다.
- → ⊆ Loc × Cond(Var) × (Act ∪ Comm) × Loc
- 기존 →는 $\text{l} \overset{g:\alpha}{\rightarrow} \text{l'}$만 있었다. 여기에 아래 2가지가 추가된다.
- $\text{l} \overset{g:c!v}{\rightarrow} \text{l'}$ : location l에서 channel c에 value v를 보내 location l'로 변함
- $\text{l} \overset{g:c?x}{\rightarrow} \text{l'}$ : location l에서 channel c에 있는 값을 x에 할당해 location l'로 변함
- 이 때 c는 P$_i$가 보낼 수 있는 channel이다.
Definition. Transition System으로 표현한 Channel System
바로 앞에서 program graph로 표현한 channel system을 살펴봤다. 이를 transition system으로 변환한 결과는 다음과 같다.


- state는 <l$_1$, l$_2$, ... , l$_n$, $\eta$, $xi$>이다. l$_i$는 P$_i$의 location이고 $\eta$는 variable evaluation function, $\xi$는 channel evaluation function이다.
- 따라서 S = (Loc$_1$ × Loc$_n$) × Eval(Var) × Eval(Chan)이다.
- 각 program graph의 위치, 각 program graph의 변수 값, 각 channel의 값이 state가 된다는 뜻이다.
- $\eta$는 Var과 $\bigcup_{x \in Var}^{} Dom(x)$ with $\eta(x)$ in Dom(x)를 매핑한다.
- $\xi$는 Var과 $\bigcup_{x \in Chan}^{} Dom(c)*$ with $\xi(x)$ in Dom(c)* and $|\xi(x)| \le cap(c)*$를 매핑한다.

- transition relation는 위 그림과 같다.
- independent한 경우에는 기존 interleaving과 같이 쓰면 된다. 분자는 기존 state의 전환 중 어떤 l$_i$의 전환이 $g:\alpha$를 쓴다는 것을, 분모는 오직 l$_i$의 location만 l'$_i$로 바뀐 것을 의미한다. 이를 만족하는 제일 작은 relation이라는 뜻이다.
- 이 때 $\xi$는 변하지 않으므로 그대로 유지된다.
- asynchronous message passing은 아래와 같다. asynchronous이므로 cap(c) > 0이 전제된다.
- receiving의 경우
- $\xi$(c)의 length > 0이고, $\xi$(c)가 v$_1$...v$_k$일 때 분모는 l$_i$의 location만 l'$_i$로, channel에서 값을 가져왔으니 $\eta$와 $\xi$가 바뀐 것을 의미한다. $\eta$'는 기존 $\eta$에서 x값만 v$_1$으로 바뀐 것을, $\xi$'(c)는 channel c의 값만 v$_2$...v$_k$로 바뀌었다는 것이다.
- 분자는 g를 만족하는 transition에 대해 l$_i$의 location만 l'$_i$로 바뀐 것을 의미한다.
- channel에서 값을 꺼내오고, variable evaluation function과 channel evaluation function 2가지를 갱신하고, location을 바꾼 것이라고 이해하면 된다.
- sending의 경우 - receiving의 경우와 같다.
- $\xi$(c)의 length ≤ cap(c)이고(빈 공간이 있고), $\xi$(c)가 v$_1$...v$_k$일 때 분모는 l$_i$의 location만 l'$_i$로, channel에 값을 넣었으니 $\xi$만 바뀐 것을 의미한다. $\xi$'(c)는 channel c의 값만 기존 $\xi$(c)에서 v가 추가되어 v$_1$...v$_k$v로 바뀐 것으로 바뀐 것을 의미한다. 변수 값이 바뀌지 않았으므로 $\eta$는 바뀌지 않는다!
- 분자는 g를 만족하는 transition에 대해 l$_i$의 location만 l'$_i$로 바뀐 것을 의미한다.
- channel에 값을 넣고, channel evaulation function과 locaiton을 갱신했다고 이해하면 된다.
- receiving의 경우
- synchronous message passing은 다음과 같다.
- synchronous message passing은 2개의 location이 동시에 바뀌어야 한다는 뜻이다.
- program graph i는 message를 receieve하고, program graph j는 message를 send한다.
- 분자가 의미하는 것은 g$_1$과 g$_2$를 만족할 때 서로 다른 program graph가 message를 주고받는 것을 의미한다.
- 분모는 이 transition으로 i, j의 location이 바뀌는 것, 그리고 변수 값도 달라졌으므로 $\eta$도 바뀐 것을 의미한다. $\eta$'는 $\eta$에서 x값만 v로 바뀌었다. $\xi$는 변하지 않는다!
- independent한 경우에는 기존 interleaving과 같이 쓰면 된다. 분자는 기존 state의 전환 중 어떤 l$_i$의 전환이 $g:\alpha$를 쓴다는 것을, 분모는 오직 l$_i$의 location만 l'$_i$로 바뀐 것을 의미한다. 이를 만족하는 제일 작은 relation이라는 뜻이다.
- Act, I(초기 state), AP, L는 program graph를 transition system으로 변환하는 것과 동일하며 따로 추가되는 것이 없다.
Variation
- c!v의 경우, c!expr처럼 변수 하나의 값이 아니라 expression의 결과값도 보낼 수 있다.
- $\text{l} \overset{c?x:\alpha}{\rightarrow} \text{l'}$처럼 communication을 condition으로 쓸 수 있다. 이 경우는 channel에서 값을 꺼내왔을 때만 $\alpha$ action을 수행하는 것을 의미한다. 값을 꺼내 오는 것은 channel에 값이 있을 때만 가능하므로 이를 조건으로 쓴 것이다.
- 기존에는 closed channel system을 [ P$_1$ | P$_2$ | ... | P$_n$ ]처럼 작성했는데, 외부와 통신하는 open channel system을 P$_1$ | P$_2$ | ... | P$_n$로 표기할 수 있다.
State Explosion
2개의 program graph가 있고, 각각 2개의 location이 있고, 2개의 shared variable이 있다고 하자. 이 때 두 program graph는 capacity 10짜리 channel이 2로 communication한다. (편의상 모든 변수는 boolean이라 두자.)
이 경우 state의 개수는 어떻게 될까?
Loc에 해당하는 state는 2 * 2이고, $\eta$에 해당하는 state도 2 * 2, $\xi$에 해당하는 state는 (2$^{11}$ - 1) * (2$^{11}$ - 1)개이다. 이 3가지의 곱이 전체 state의 개수이다. 너무 크다! 만약 unbounded channel인 경우에는 당연히 INF이다. 이 문제를 해결하는 방법은 추후에 알아본다.
(nano)promola
위에서 배운 수식들은 수학적 도구를 사용하기 때문에 너무 복잡하다. 때문에 더 간단한 형식으로 써야 하는데, 이 형식은 비전문가도 사용하지 않을 정도로 간단해야 하지만 의미를 정확하게 나타내야 한다. 이를 언어로 표현하는 방식 중 하나가 promela이다.
promela는 model checker 중 하나인 SPIN의 input language이다.
SPIN의 동작 방식은 다음와 같다.
- 사용자가 promela program을 작성한다.
- promela program은 channel system을 매핑한 것으로써, 적당한 syntax를 사용해 이를 쓸 수 있다.
- SPIN은 사용자가 작성한 promela program을 channel system으로 바꾼다.
- 변환된 channel system을 transition system으로 바꾼다.
- transition system에서 model checking을 진행한다.
nanopromela program $\overline{P}$ = [ P$_1$ | P$_2$ | ... | P$_n$ ]일 때, 각 P$_i$를 process라고 한다. process의 동작을 의미하는 statement의 syntax는 다음과 같다.
nanopromela에서 변수 선언, dynamic process 생성 등 detail 등을 사용하지 않는다.
| stmt ::= skip | x := expr | c?x | c!expr | stmt$_1$; stmt$_2$ | atomic{assignments} | if :: g$_1$ $\Rightarrow$ stmt$_1$ ... :: g$_n$ $\Rightarrow$ stmt$_n$ fi | do :: g$_1$ $\Rightarrow$ stmt$_1$ ... :: g$_n$ $\Rightarrow$ stmt$_n$ od | |
여기서 사용하는 syntax들은 channel system에서 사용하는 것과 동일하므로 쉽게 이해할 수 있을 것이다.
- skip : atomic command를 의미한다.
- x := expr : assignment
- c?x, c!expr : channel에 push/pop
- atomic{} : atomic operations
- if : guard 조건을 만족할 때 branch
- 만약 else option이 없는 경우는 stmt를 skip으로 두면 if branch를 탈출한다.
- do : guard 조건을 만족할 때 loop
- n개의 guard 중 1개 이상이 true가 될 때까지 loop를 돌린다.
유의점
1. test-and-set semantics
promela에서 선언한 [guard에 대한 evaluation + enabled guard의 선택 + 선택된 guard에 해당하는 첫 번째 atomic statement의 실행] 이 3가지 동작은 program graph에서 하나의 edge가 된다.
- 예를 들어 guard가 x>=0, x<=0이 있는 상황이라면 어떤 statement를 실행해야 할까? 이를 위해 test-and-set semantics를 사용한다. x의 값을 보고, enabled guard를 non-determinsitic하게 고르고, 해당 guard의 첫 번째 atomic statement를 실행한다. 이 모든 것이 한 edge가 된다.
2. blocking semantics
if문에서 guard가 만족되지 않는 경우, 빠져나가지 않고 만족될 때까지 기다린다! blocking semantics는 if문에서만 적용된다.
| if x > 10 $\Rightarrow$ atomic{...} x < 4 $\Rightarrow$ atomic{...} fi |
직관적이지 않기 때문에 nanopromela 예시를 들어 보자.
x가 7이라고 하자. 그러면 if문의 모든 guard가 false이기 때문에 if가 시작되지 직전 위치에서 기다린다. x가 shared variable이라고 하면, 다른 process에서 값을 바꿀 수 있고, 그러면 guard가 true로 되기 때문이다. 원칙적으로는 무한히 기다릴 수 있다.
정리
- interleaving `|||`
- shared variable과 independent한 transition system의 경우 transition system의 interleaving TS$_1$ ||| TS$_2$로 표현한다.
- shared variable를 사용하는 경우 program graph의 interleaving P$_1$ ||| P$_2$를 transition system으로 변환한다.
- synchronous message passing (handshaking) ||$_H$
- H에 속해있는 action만 synchronization이 일어날 때 TS$_1$ ||$_H$ TS$_2$로 표기한다.
- channel system
- interleaving, shared variable, message passing 3가지가 모두 속해 있다.
- buffer size에 따라 synchronous message passing인지 asynchronous message passing인지가 결정된다.
- [ P$_1$ | P$_2$ | ... | P$_n$ ]로 표기하며 이 결과를 transition system으로 변환한다.
'Project > Model Checking' 카테고리의 다른 글
| [Maude] Token Ring 검증 (0) | 2023.10.23 |
|---|---|
| [Model Checking] Designing Reliable Distributed Systems (0) | 2023.10.09 |
| [Model Checking] 과제연구 주제 정리 (0) | 2023.09.19 |
| [Model Checking] Linear Time Properties (0) | 2023.09.19 |
| [Model Checking] Transition System과 Program Graph (0) | 2023.09.11 |
![[Model Checking] Modeling Concurrent System](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FVV522%2FbtstG7YHEdh%2FXGMgfm7J6xbZVTbRUwsW2k%2Fimg.png)