PS/PS Log
23.05.09. 풀었던 문제들
hyelie
2023. 5. 9. 10:22
Leetcode 54. Spiral Matrix
첫 접근 (wrong)

처음에는 위 그림처럼 풀려 했다. 결국 spiral로 풀기 때문에 겉면만 벗겨가면서 풀면 된다고 생각했기 때문이고, 가능하면 모든 변을 동일하게 접근하는 게 구현에서 쉬울 거라 생각했다.
일단 벗기는 회수는 row size를 m, col size를 n이라 했을 때 min((m+1)/2, (n+1)/2)이다. 이건 뭐 간단하게 나오는 답.
그러나 복잡한 경우는 matrix가 3 by 3라서 제일 겉면을 벗겼는데, 안에 딱 1개의 element만 남는 경우이다. [시작점]부터 [끝점-1]까지만 접근하기 때문에 이런 경우를 처리할 수 없다.
올바른 접근 (correct)
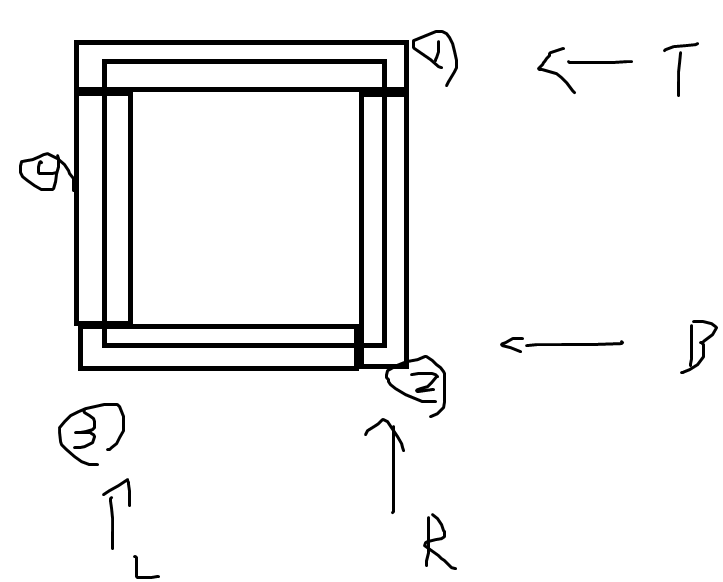
결국 한 번은 전부 다에 접근해야 한다. 구현의 편의를 위해 row 시작점/끝점, col 시작점/끝점의 좌표를 기억하자. 그리고 자연스럽게 spiral로 돌리면 위 그림처럼 돌게 된다.
각 탐색이 끝나면 해당 위치는 더 이상 탐색하지 않기에 그 값을 갱신한다.
- 처음에는 rowStart row에 있는 모든 element를 담는다. [rowStart, 0], [rowStart + 1, 0] , ... , [rowEnd, 0]이 그것이다. 이 탐색이 끝나면 rowStart++해준다.
- 다음으로 colEnd col에 있는 모든 element를 담는다. [1, colEnd], [2, colEnd], ... , [rowEnd, colEnd]가 그것이다. 이 탐색이 끝나면 해당 colEnd는 더 이상 탐색하지 않으므로 colEnd--해 준다.
- 같은 방법으로 아래쪽을 벗긴다. 이 때, rowStart가 rowEnd와 같으면 위쪽과 같은 row를 탐색하는 것이므로 패스한다.
- 같은 방법으로 왼쪽을 벗긴다 .이 때 colStart가 colEnd와 같으면 오른쪽과 같은 col을 탐색하는 것이므로 패스한다.
// Runtime 0 ms Beats 100%
// Memory 6.8 MB Beats 69.57%
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size(), cnt = 0;
vector<int> answer;
int numRepeat = min((m+1)/2, (n+1)/2);
int rowStart = 0, rowEnd = m-1, colStart = 0, colEnd = n-1;
for(int k = 0; k<numRepeat; k++){ // cycle 시작지점이 몇 개인지
for(int j = colStart; j<=colEnd; j++){
answer.push_back(matrix[rowStart][j]);
}
rowStart++;
for(int i = rowStart; i<=rowEnd; i++){
answer.push_back(matrix[i][colEnd]);
}
colEnd--;
if(rowEnd >= rowStart){
for(int j = colEnd; j>=colStart; j--){
answer.push_back(matrix[rowEnd][j]);
}
rowEnd--;
}
if(colEnd >= colStart){
for(int i = rowEnd; i>=rowStart; i--){
answer.push_back(matrix[i][colStart]);
}
colStart++;
}
}
return answer;
}
};
시간복잡도
결국 모든 matrix를 순회해야 하므로 row size를 m, col size를 n이라 할 때 O(mn)이다.
공간복잡도
추가 공간은 사용하지 않으므로 O(1)
후기
구현 빡세..