[이종병렬컴퓨팅] Parallel Patterns : Reduction

CS/Parallel Computing

[이종병렬컴퓨팅] Parallel Patterns : Reduction

hyelie 2023. 12. 16. 03:35

이 글은 포스텍 성효진 교수님의 이종병렬컴퓨팅(CSED490C) 강의를 기반으로 재구성한 것입니다.

이 글에서는 parallel reduction pattern을 살펴본다.

parallel reduction pattern은 제일 많이 사용되는 패턴 중 하나이다. 추가로, control divergence와 thread utilization 등의 작업 효율성, shared memory bank conflict 등의 resource 효율성을 살펴본다.

Reduction

Reduction은 input value를 하나의 값으로 요약하는 연산이다. 예를 들어 max(), min(), sum() 등등이 있다.

기본적으로 associative(결합), commutative(교환)여야 하며, 잘 정의된 identity value가 있어야 한다.

identity value는 항등원을 의미한다. sum의 경우 0, product의 경우 1, 등등이다.

Partition and Summarize

큰 input data set을 처리할 때 자주 사용되는 전략이다. 순서는 다음과 같다.

data set의 element를 처리할 때 특별한 순서가 없으므로, input data set을 작은 chunk로 분할한다.
이후 각 thread가 chunk를 담당한다.
각 chunk로부터 reduction 결과를 tree를 만들어 최종 결과를 만든다.

Reduction은 다른 기술들도 가능하게 만든다.

몇몇 연산의 경우, 병렬 변환 이후 reduction이 필요하다.

예를 들어 지난 포스팅에서 살펴봤던 histogram의 privatization의 경우, 각 thread block에서 private copy를 만들었다. 이후 private copy를 사용해 final copy를 만들 때 reduction tree를 사용한다.

Sequential Reduction

sequential reduction은 다음과 같이 실행한다.

reduction operation의 초기값을 identity value로 설정한다.
- 예를 들어 max의 경우 제일 작은 값을(INT_MIN), min의 경우 제일 큰 값을(INT_MAX), sum의 경우 0, product의 경우 1로 설정하는 것이 그것이다.
input을 순회하면서 n개의 입력에 대해 n번 reduction 연산을 수행한다.

이 경우 각 element는 오직 1번만 방문하므로 O(n) 알고리즘이다.

Parallel Reduction Tree

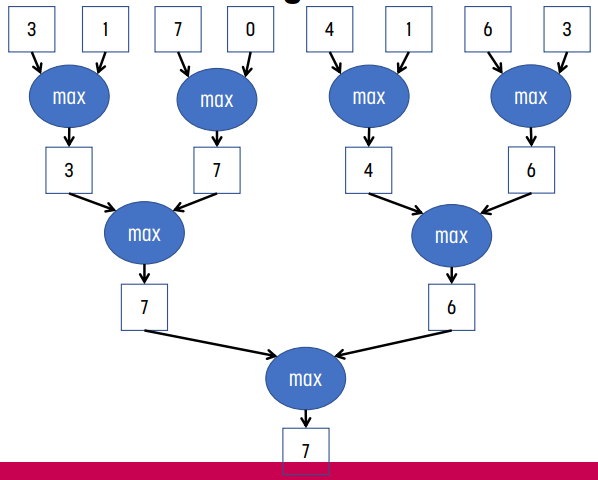
반면 parallel reduction tree는 각 reduction의 결과를 tree로 만들어 합치는 방법이다.

Reduction Tree 알고리즘 분석

n개의 입력 값이 있을 때, binary reduction을 사용하는 reduction tree의 경우, 첫 번째 pass에서는 n/2번, 두 번째 pass에서는 n/4번, ... 마지막 pass에서는 1번의 연산을 수행한다. 즉 (1/2 + 1/4 + 1/8 + ... + 1/n) * n = (1 - 1/n) * n = n - 1번의 연산을 수행하게 된다.

pass는 총 logn개가 있게 된다.

따라서 평균 parallelism은 $\frac{n-1}{logn}$이다.

예를 들어 n이 1,000,000일 때 20개의 pass가 생긴다. 이 때 평균 parallelism은 50,000인 반면 첫 번째 pass에서는 500,000번의 연산이 필요하다. 이처럼 이 방식은 work-efficient한 방식이지 resource-efficient한 방식이 아니다.

GPU에서 Parallel Reduction

GPU에서 parallel reduction은 다음과 같은 과정을 거쳐 수행된다.

각 thread block에서 tree-based 알고리즘을 사용한다.
- 이 때 각 thread block에서는 shared memory를 사용해 in-place reduction을 수행한다고 가정하자. (모든 thread는 병렬로 수행되기 때문) 즉, global memory에 있는 값을 shared memory에 load하고, thread block에서 reduction을 수행한다고 가정하자는 것이다.
그러면 original data set은 global memory에 존재하게 되고, thread block의 shared memory는 일부 값만 가진다.
- 예를 들어 이 때 sum()을 실행한다고 했을 때, 각 pass에서 partial sum을 계산하고, 그 결과는 index 0에 저장될 것이다.(이 값은 최종 결과값에 반영될 것이다) 이를 통해 global memory access 회수를 줄일 수 있다.
매우 큰 값을 처리하기 위해서는 여러 개의 thread block을 사용해야 한다. 이는 GPU를 BUSY한 상태로 유지하는 것에서도 의미가 있게 되고, 각 thread block은 input data set의 일부 값을 처리하게 된다.

Reduction #1 : Interleaved Addressing

제일 기본적인 버전으로, element to thread direct mapping라고도 불린다.

다음과 같은 단계로 실행된다.

각 thread는 shared memory에 값을 할당한다. (모든 thread가 shared memory에 data를 올리는 과정에 참여한다.)
각 pass에서 2개의 값을 더하며, pass마다 stride를 2배로 늘린다.
- 첫 번째 iteration에서는 홀수 thread들이 자신에 해당하는 값과 인접한 값에 대해 reduction을 수행한다.
동시에 각 pass마다 thread 개수를 절반으로 감소시켜가면서 재귀적으로 반복한다.

즉, n개의 element를 처리하기 위해 logn의 pass와 n개의 thread가 필요하다.

예를 들어 pass 1에서는 0 2 4 6 ...의 thread만, pass 2에서는 0 4 8 12, ...의 thread만, pass 3에서는 0 8 16, ...의 thread만 계산에 참가한다.

CUDA Kernel

각 thread는 자신이 담당하는 부분에 대한 책임을 가진다.
각 pass가 끝나면 절반의 thread는 더 이상 필요가 없어진다.
각 pass에서, 2개의 값을 더하는데, 하나는 그 thread가 생성한 값이고, 다른 하나는 다른 thread가 처리한 값인데, 이 때 다른 하나의 입력값이 점점 더 멀리서 온다.
- pass 0에서는 바로 옆에서 오지만 pass 1에서는 2칸, pass 2에서는 4칸, pass 3에서는 8칸, ... 이렇게 입력값이 멀리서 온다.

__global__ reduction(int *input, int *results) {
    unsigned int t = threadIdx.x;
    unsigned int i = blockIdx.x * blockDim.x + threaddIdx.x;

    __shared__ float partialSum[BLOCK_SIZE]; // BLOCK_SIZE == blockDim.x
    partialSum[t] = input[i]; // 각 thread가 하나의 element를 shared memory에 load한다.

    for (unsigned int stride = 1; stride <= blockDim.x; stride *= 2) {
        __syncthreads();
        if (t % (2 * stride) == 0){
            partialSum[t] += partialSum[t + stride];
        }
    }

    // 여기에 __syncthread()를 추가하지 않는 이유?
    // thread 0이 결과를 적는다.
    if (t == 0) {
        // note that the result is per-block, not per-thread
        results[blockIdx.x] = partialSum[0];
    }
}

각 thread block는 blockDim.x개의 input element를 처리하고, 각 thread는 1개의 element를 shared memory에 올린다.
for문 내의 `__syncthread()`가 필요한 이유는 이전 pass의 partial sum이 모두 계산되어 있어야 하기 때문이다.
마지막 loop가 끝난 후 `__syncthread()`를 추가하지 않는 이유는, `if(t == 0)`으로 왔다는 것은 이미 partialSum을 모두 계산한 것이기 때문이다.

그리고 위 코드의 제일 마지막에 있는 `results[blockIdx.x] = partialSum[0]`의 경우, 모든 input에 대한 결과값이 아니라 해당 thread block의 결과이다. 최종 결과값을 얻기 위해서는 reduction이 다시 한 번 수행되어야 한다.

Observation

각 iteration에서, 각각의 warp에 대해 2개의 control flow가 순차적으로 발생한다. 하나는 for문 내의 if문에 걸려서 addition을 수행하는 thread들, 나머지는 그렇지 않은 thread들이다. 그렇지만 아무것도 하지 않는 thread들도 여전히 resource를 소모하고 있다. (idling)

첫 번째 pass가 끝나면 절반의 thread가 필요없게 된다. 즉, 모든 홀수 index를 가지는 thread는 첫 번째 pass가 끝난 이후 필요없게 된다.

예를 들어 n이 1024인 경우, 5번째 pass가 끝나면 전체 warp의 각 block은 for문 내의 if문을 실패하게 되어 resource utilization이 별로다. 몇몇 warp는 살아있을 수 있지만, 해당 warp에서 오직 하나의 thread만 if문을 성공하므로 divergence가 발생한다.

예를 들어 thread block size가 32인 경우, 5번째 pass 이후에는 active thread의 간격이 64가 되는데, 그러면 thread block 0의 첫 번째 thread는 active, thread block 1의 모든 thread는 inactive, 이후 thread block 2의 첫 번째 thread가 active, ... 이렇게 반복된다. 때문에 warp의 일부 thread block의 모든 thread는 idling하게 된다.

Reduction #2 : Interleaved Addressing 2

이 방식은 n개의 element에 대해 logn개의 pass를 사용하되, n/2개의 thread만 사용하는 방식이다.

각 thread block은 2 * blockDim.x개의 input element를 처리하고, 2개의 element를 shared memory에 load한다. 위 그림에는 바로 옆에 있는 값을 shared memory로 load하는 것으로 보이는데, 실제로는 thread 하나는 threadIdx.x와 threadIdx.x + BLOCK_SIZE 2개의 값을 shared memory로 load하는 방식이다. 이렇게 하면 memory coalescing을 통해 조금이나마 더 효율적으로 작동한다.

그 결과 divergence를 조금 줄일 수 있다.

CUDA Kernel

__global__ reduction(int *input, int *results) {
    __shared__ float partialSum[2 * BLOCK_SIZE]; // BLOCK_SIZE == blockDim.x
    
    // load two elements
    unsigned in t = threadIdx.x;
    unsigned int start = (2 * BLOCK_SIZE) * blockIdx.x;
    partialSum[t] = input[start + t];
    partialSum[BLOCK_SIZE + t] = input[start + BLOCK_SIZE + t];

    for (unsigned int stride = 1; stride <= blockDim.x; stride *= 2) {
        __syncthreads();
        if (t % stride == 0){
            partialSum[2 * t] += partialSum[2 * t + stride];
        }
    }

    // thread 0이 결과를 적는다.
    if (t == 0)
    {
        // note that the result is per-block, not per-thread
        results[blockIdx.x] = partialSum[0];
    }
}

#1과의 차이점은 for문 내의 if문이다.

한편 이 경우 2-way bank collision이 발생한다.

Reduction #3 : Non-Divergent Reduction

#1 버전과 달라진 점은 thread id가 순서대로 줄어든다는 것이다. 이를 통해 하나의 warp에 있는 thread를 계속 살릴 수 있게 되므로 divergent가 줄어든다.

CUDA Kernel

reduction #1에서 inner loop의 divergent branch를 없애고, strided index와 non-divergent branch를 사용한다.

for (unsigned int stride = 1; stride <= blockDim.x; stride *= 2) {
    __syncthreads();
    int index = t * (2 * stride);
    if (index < blockDim.x) {
        partialSum[index] += partialSum[index + stride];
    }
}

단, 이 경우에는 shared memory bank conflict가 발생한다. 첫 번째는 2-way, 두 번째는 4-way, ... 이렇게 bank conflict가 계속 늘어난다.

thread index의 사용이 문제다

divergence를 없애기 위해 index를 바꿔서 쓸 수도 있다. 물론 이 경우는 commutative나 associative여야만 한다.

#3 버전의 경우에는 active thread가 연속적이지만 접근하는 data가 멀리 있기 때문에 bank conflict가 발생한다는 점도 문제였다.

더 좋은 전략은 항상 partialSum[] 배열의 첫 번째 위치로만 partial sum을 합치는 것이다. 이를 통해 active thread를 연속적으로 유지할 수 있다.

Reduction #4 : Sequential Addressing

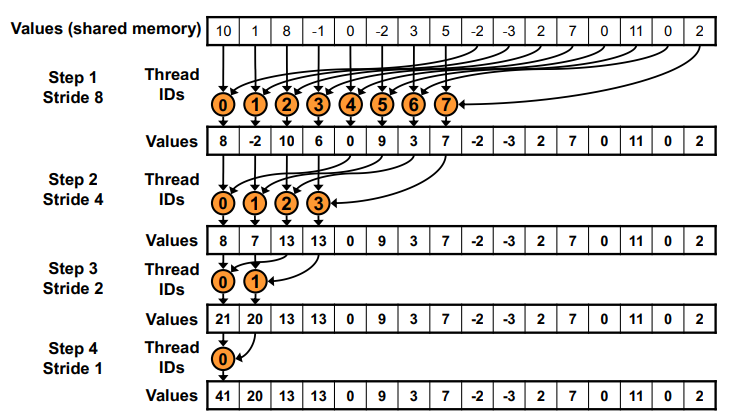
#3까지의 구현은 stride가 점점 더 커지는 방식이었다. 그러나 sequential addressing의 경우에는 stride가 점점 더 줄어든다. 이것이 더 좋은 이유는 bank conflict가 없어지기 때문이다.

CUDA Kernel

그러면 코드는 아래와 같다. 바뀐 점은 stride의 초기값, 바뀌는 값, 그리고 partialSum의 index이다.

// before : #1 interleaved addressing
for (unsigned int stride = 1; stride <= blockDim.x; stride *= 2) {
    __syncthreads();
    if (t % (2 * stride) == 0){
        partialSum[t] += partialSum[t + stride];
    }
}

// before : #3 non-divergent reduction
for (unsigned int stride = 1; stride <= blockDim.x; stride *= 2) {
    __syncthreads();
    int index = t * (2 * stride);
    if (index < blockDim.x) {
        partialSum[index] += partialSum[index + stride];
    }
}

// after : #4 sequential addressing
for (unsigned int stride = BLOCK_SIZE / 2; stride >= 1; stride /= 2) {
    __syncthreads();
    if (t < stride){
        partialSum[t] += partialSum[t + stride];
    }
}

before의 경우에는 bank conflict가 발생하지만 after의 경우에는 그렇지 않는다. 그리고 stride가 *2에서 /2로 바뀌었다. 또한 if문의 condition이 달라진다.

분석

예를 들어 thread block size가 32일 때 1024개의 thread가 있는 thread block의 경우, 각 thread block은 1024개의 element를 shared memory에 올린다.

이 때 처음 5개 group에 대해서는 divergence가 존재하지 않는다! 512, 256, 128, 64, 32개의 연속된 32개의 thread들이 각 pass에서 계속 active하기 때문에, warp 내의 모든 thread가 active거나 모두 inactive이기 때문이다.

반면, 이후 16, 8, 4, 2, 1 5개 step에 대해서는 divergence가 발생한다.

다시 Global하게 돌아가면 : Segmented Reduction

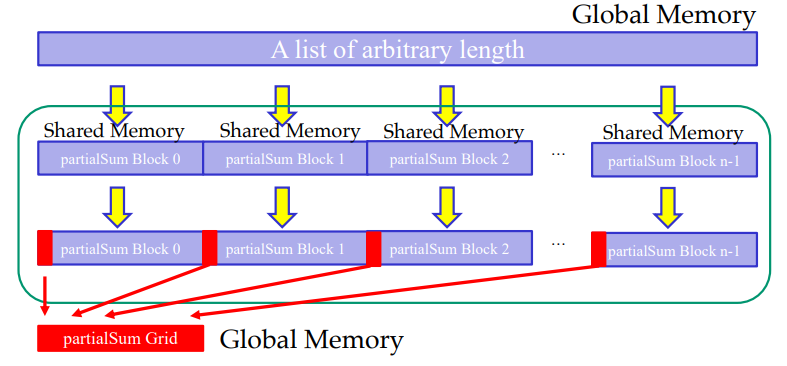
kernel 실행이 끝났을 때, 각 thread block의 오직 단 하나의 thread, thread 0만이 partialSum[0]에 있는 값을 global result의 blockIdx.x에 작성한다. 이후 이 global result에 다시 한 번 reduction을 진행해야 한다.

만약 input vector size가 매우 큰 경우, host는 반복적으로 kernel code를 실행시켜야 한다.
- global memory에 저장된 처음의 reduction 결과도 여전히 클 때, 그 reduction 결과에 대해 반복적으로 reduction을 진행한다는 말이다.
- 또는, global sum을 만들기 위해서는 atomic operation을 사용할 수도 있다. 단 이 경우에는 reduction 결과가 atomicAdd를 사용해도 될 만큼 충분히 작아야 할 것이다.
만약 input vector size가 별로 크지 않은 경우, data를 kernel로 전송하고 다시 불러오는 간단한 과정만 거쳐도 된다.

Parallel Algorithm 분석

Parallel Algorithm Overhead

parallel하게 reduction을 실행했을 때 overhead는 1) shared memory에 값을 올리는 것과 2) reduction을 실행하는 for문에 존재하는 barrier(__syncthread())에 대한 overhead가 있다.

또한, asymtotic하게 연산의 개수는 O(n)이지만, 각 연산은 주소 계산이나 중간 결과값 조작 등 복잡한 로직을 포함하고 있다.

이러한 점 때문에 만약 parallel code가 single thread hardware에서 실행된다면 sequential algorithm보다 훨씬 느릴 것이다.

Parallel Reduction Complexity

logn번의 parallel pass에 대해, 각 pass S는 $\frac{n}{2^S}$번의 독립적인 연산을 수행한다. 즉, step complexity(pass의 개수)는 O(logn)이다. 그리고 각 pass에서는 O(n)의 연산이 수행된다.

물리적으로 병렬로 동작하는 P개의 thread에 대해, time complexity는 O($\frac{n}{P}$ + logn)이다.

$\frac{n}{P}$ 부분은 전체 작업량을 processor의 개수로 나눈 부분이다.
logn 부분은 step complexity 부분이며, 해당 부분은 parallelize될 수 없으므로 logn이다.
한편, thread block에서 n = P이므로 O(logn)이다.

parallel algorithm의 cost는 processor의 개수 * time complexity이다. 즉 O(n) thread * O(logn) time complexity = O(nlogn)이다. 즉, cost-inefficient이다. (sequential의 경우 O(n)라는 것을 기억하자.)

즉, sequential한 버전보다 parallelize에 추가적인 resource가 필요해 더 많은 resource를 사용하고, 더 많은 시간이 걸린다.

Algorithm Cascading

sequential과 parallel을 결합할 수 있다.

지금까지 살폈던예시에서는 각 thread가 binary reduction을 수행하는 예시를 보았지만, 더 효율적인 병렬화를 위해 각 thread가 2개 이상의 element를 shared memory에 load하고 합칠 수 있다. 같은 방식으로 binary reduction 대신 n-way reduction을 수행한다.

이것이 cascading인데, 각 thread는 sequential하게 실행하는 element의 개수가 늘어나므로 thread 자체의 실행 시간은 더 길어지지만 pass의 개수가 줄어든다. 전체적으로 시간이 훨씬 더 많이 줄어드므로, 더 효율적이게 된다.

단계로 표현하면 다음과 같다.

각 thread는 sequential하게 O(logn)개의 element를 합친다.
그러면 O($\frac{n}{logn}$)개의 thread를 할당했을 때, O($\frac{n}{logn}$)개의 thread는 O(logn) pass에 대해 parallelize하게 실행된다.
따라서 cost = O($\frac{n}{logn}$ * logn) = O(n), 즉 cost-efficient하다.
- thread 개수가 $\frac{n}{logn}$개, 각 thread는 logn개만큼 연산을 수행하기 때문.

이 경우 parallelism과 overhead이 균형을 이루며, 실제로는 상당한 속도 향상이 이뤄진다.

추가적인 최적화 #5 : Unroll Loops

reduction은 낮은 arithmetic intensity를 가지고 있으므로, bandwidth를 포화할 수 있다.(계산에 필요한 연산량보다 I/O를 더 많이 쓴다는 뜻이다) 따라서 bottleneck은 instruction overhead일 가능성이 높다. 즉 address array arithmetic과 loop overhead이다.

그러면 loop를 없애면 된다!

reduction이 진행될 때마다 active thread의 개수가 감소한다. 특히 stride <= 32일 때는 오직 하나의 warp의 thread 중 몇 개만 active하다. 이 때 instruction은 warp 내에서 SIMD 방식으로 동기화되고, lock-step에서 실행된다. 즉, stride <= 32일 때 warp끼리 barrier를 사용할 필요가 없고, 같은 이유로 `if(t < stride)`도 필요없다.

그러면 마지막 6개의 iteration(32, 16, 8, 4, 2, 1)에 대해서는 loop를 풀면 더 효율적일 것이다.

CUDA Kernel

// for stride > 32
for (unsigned int stride = BLOCK_SIZE / 2; stride > 32; stride /= 2) {
    __syncthreads();
    if (t < stride)
        partialSum[t] += partialSum[t + stride];
}

// loop unrolling for stride <= 32
if (t < 32) {
    partialSum[t] += partialSum[t + 32];
    partialSum[t] += partialSum[t + 16];
    partialSum[t] += partialSum[t + 8];
    partialSum[t] += partialSum[t + 4];
    partialSum[t] += partialSum[t + 2];
    partialSum[t] += partialSum[t + 1];
}

이 방식은 마지막 warp 뿐만 아니라 모든 warp에서 필요 없는 작업을 없앤다. unrolling하지 않는 경우, 모든 warp에서 for loop와 if문을 반복적으로 실행한다.

실행 시간 분석

각 버전에 대해 실행 결과는 위와 같다.

kernel 1 : #1 버전
kernel 2 : #3 버전
kernel 3 : #4 버전
kernel 4 : 이 글에서 다루지 않음
kernel 5 : #5 버전

잘못된 내용이나 오탈자에 대한 지적, 질문 등은 언제나 환영합니다.

저작자표시