그래프 알고리즘 - (5) Minimum Spanning Tree(Kruskal, Prim)
이 글은 포스텍 오은진 교수님의 알고리즘(CSED331) 강의를 기반으로 재구성한 것입니다.
1. Minimum Spanning Tree
정의
MST는 모든 vertex를 포함하면서 weight를 최소화한 tree이다. 이는 greedy하게 구할 수 있으며, Kruskal과 Prim 2가지 방법으로 구할 수 있다.
2. Kruskal Algorithm
Cut Property
MST T에 속해있는 edge들의 부분집합 X에 대해, X가 속해있는 영역 S와 나머지 영역 V\S로 나눈다. e가 S와 V\S를 weight가 가장 작은 edge라고 하자. 그러면 X ∪ {e}는 MST의 부분집합이 된다.
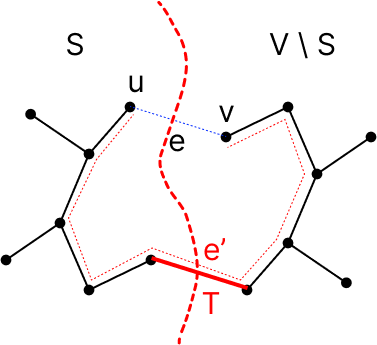
proof)
e가 MST T의 일부라면 X ∪ {e}는 T의 subset인 것은 자명하다.
그렇지 않고 T가 e 대신 e'을 포함한다고 가정하자. 그러면 이 때 새로운 MST T' = T ∪ {e} - {e'}을 만들어 보면, Cost(T') <= Cost(T)이므로 T'이 MST이다.
Correctness of Kruskal Algorithm
kruskal algorithm은 모든 edge 중 weight가 작은 것부터 고른다. 다만 tree - connected acyclic graph - 를 찾는 것이기 때문에 cycle이 생기면 안된다. -를 반복해 MST를 만드는 방법이다.
증명은 바로 위의 cut property를 이용해 증명할 수 있다. cycle을 만들지 않는 lightest weight edge를 고르는데, 이 edge가 cross edge이므로 이러한 edge들만 골라가면 MST가 만들어 진다는 것이다.
cycle을 형성하는지 여부는 union-find로 해결할 수 있다.
코드 : O(VlogV)
Struct Edge{
int from, to, weight;
}
int Parent[1000001];
int Rank[1000001];
void Makeset(int s){
Parent[s] = s;
Rank[s] = 0;
return;
}
int Find(int x){
if(x == Parent[x]) return x;
Parent[x] = Find(Parent[x]); // x의 parent를 x의 root로 설정
return Parent[x];
}
void Union(int x, int y){
int rx = Find(x);
int ry = Find(y);
if(rx == ry) return;
if(Rank[rx] < Rank[ry]) // ry의 height가 더 크면 rx가 밑으로 글어가야 함
Parent[rx] = ry;
else{ // 그렇지 않다면 ry가 밑으로 들어가야 함
Parent[ry] = rx;
if(Rank[rx] == Rank[ry]){ // rank가 같으면 rank 조절
Rank[ry]++;
}
}
}
void Kruskal(vector<Edge> edges){
vector<Edge> MST;
sort(edges.begin(), edges.end()); // edge 정렬
for(Edge e: edges){ // 모든 edge에 대해
if(find(e.from) != find(e.to)){ // cycle 형성하지 않으면 MST에 push
MST.push_back(e);
Union(edge.from, edge.to); // Union 연산
}
}
}
시간복잡도
전체 edge를 오름차순 정렬하는 데 O(ElogE), kruskal algorithm은 edge를 고르는 것이니 Worst O(E).
find(x)는 2|E|번, union(x, y)는 |V|-1번 호출되고 path compression을 한 union-find의 경우 각각의 operation이 O(log*|V|)이므로 O(|E| log*|V|). 보통 graph의 경우 |E| >= |V|이므로 따라서 모두 합쳐 O(ElogE)이다.
3. Prim Algorithm
prim 알고리즘도 MST를 구하는 방법 중 하나이다. kruskal의 경우 모든 edge 중 cycle을 만들지 않는 lightest edge만 골랐다면, prim은 아래와 같은 순서를 따른다.
- 아무 vertex나 MST set에 넣는다.
- MST set의 크기가 |V|가 될 때 까지 아래 과정을 반복한다.
- MST set에 속해있는 모든 vertex의 edge 중 lightest edge를 골라 그 edge와 연결된 vertex를 MST set에 넣는다. 다만, 그 vertex가 MST set에 속해있으면 cycle이 만들어지기 때문에 그 edge는 넘긴다.
kruskal과 비슷하다. acyclic하게 만들기 위해 이미 뽑은 vertex를 탐색한다면 넘기고, 그렇지 않다면 해당 edge를 골라 MST에 넣는 것이다.
코드 : O(ElogV)
struct cmp{
bool operator()(pii &a, pii &b){
return a.second > b.second;
}
};
// edges[i] : i가 edge의 시작인 edge list
// edges[i][0].first : edge list의 edge end
// edges[i][0].second : edge list의 edge weight
int Prim(vector<vector<pii>> edges){
int cost = 0;
set<int> MST;
priority_queue<pii, vector<pii>, pqcmp> pq; // pii.first : edge end, pii.second : edge weight
// 시작 vertex
MST.insert(0);
for(pii p : adjacent[0]){
pq.push(p);
} // 시작 vertex와 연결된 모든 edge를 pq에 넣는다.
while(MST.size() < V.size()){ // MST size가 |V|이 될 때까지 반복
pii p = pq.top(); pq.pop();
if(MST.find(p.first) == MST.end()){ // 연결되지 않았다면 연결
MST.insert(p.first);
cost += p.second;
for(pii next_edges : edges[p.first]){
pq.push(next_edges);
}
}
}
return cost;
}
시간복잡도
set에 V를 넣고 검사하는 데 O(VlogV), edge의 for문이 |E|번 수행되므로 O(ElogV)이다.
4. Kruskal vs Prim
| Kruskal | Prim |
| O(ElogE) | O(ElogV) |
| |E|보다 |V|가 더 큰 sparse graph에 적합 | |E|보다 |V|가 더 작은 dense graph에 적합 |