약수 구하기 : O(n^0.5)
내 블로그 포스트에서 정리했다.
set<int> getFactorNumber(int n){
set<int> v;
for(int i = 1; i <= sqrt(n); i++){
if(n % i == 0){
s.insert(i);
s.insert(n%i);
}
}
return cnt;
}
소인수분해 : 소수인 경우 O(n), 합성수인 경우 O(logn)
내 블로그 포스트에서 정리했다.
vector<int> getPrimeFactorization(int n){
vector<int> v;
for(int i = 2; i <= sqrt(n); i++){
while(n % i == 0){
v.push_back(i);
n /= i;
}
}
if(n > 1) v.push_back(n);
return v;
}
최소공배수/최대공약수 LCM/GCD : log(log(min(a,b)))
내 블로그 포스트에서 정리했다. 유클리드 호제법을 이용한다.
int gcd(int a, int b){
while(b != 0){
int r = a % b;
a = b;
b = r;
}
return a;
}
int lcm(int a, int b){
return a * b / gcd(a, b);
}
이진 탐색 Binary Search, Lower Bound, Upper Bound : O(logn)
직접 구현한 것의 유의점으로 arr에 없는 값을 lower bound, upper bound로 탐색 시에는 v.size()값을 가진 end값을 리턴하므로 이를 유의해야 함. STL의 경우에는 last를 리턴.
// 직접 구현
int binary_search(vector<int>& v, int input){
int start = 0, end = v.size()-1, mid;
while(start <= end){
mid = (start + end) / 2;
if(v[mid] < input){
start = mid + 1;
} else if(v[mid] == input){
return mid; // found
} else{
end = mid - 1;
}
}
return -1; // not found
}
int lower_bound(vector<int> &v, int target)
{
int mid, start = 0, end = v.size();
while (start < end)
{
mid = (start + end) / 2;
if (v[mid] >= target) // 중간값이 target보다 크거나 같은 경우 해당 index까지 end를 당김.
end = mid;
else start = mid + 1; // 중간값이 target보다 작으면 mid+1까지 start를 당김.
}
return end;
}
int upper_bound(vector<int> &v, int target)
{
int mid, start = 0, end = v.size();
while (start < end)
{
mid = (start + end) / 2;
if (v[mid] > target) // 중간값이 target보다 큰 경우 해당 index까지 end를 당김.
end = mid;
else start = mid + 1; // 중간값이 target보다 작으면 mid+1까지 start를 당김.
}
return end;
}
// STL 이용
#include <algorithm>
binary_search(v.begin(), v.end(), value);
lower_bound(v.begin(), v.end(), value); // 결과로 iterator가 리턴됨
lower_bound(v.begin(), v.end(), value) - v.begin(); // index
upper_bound(v.begin(), v.end(), value); // 결과로 iterator가 리턴됨
upper_bound(v.begin(), v.end(), value) - v.begin(); // index
소수 판별 : O(nloglogn)
최적화된 에라토스테네스의 체 : O(nloglogn)
내 블로그 포스트에서 정리했다. 추후 더 큰 수에 대해 소수를 판별해야 하는 일이 생긴다면 그 때 추가 정리 하겠다.
typedef long long ll;
// isPrime[i] : i가 소수이면 true, 아니면 false.
void find_prime_improved(vector<bool>& isPrime, ll max_value){
vector<bool> isPrime(max_value, true);
isPrime[0] = isPrime[1] = false;
for(ll i = 2; i<=sqrt(max_value); i++){
if(isPrime[i]){
for(ll j = i*i; j<=max_value; j+= i){
isPrime[j] = false;
}
}
}
}
행렬곱 : O(n$^{3}$)
슈트라센 알고리즘까지는 아니더라도, cache를 고려한 것까지는 기억해 두자. KIJ
- i : arr1의 row idx
- j : arr2의 col idx
- k : arr1의 col, arr2의 row idx
vector<vector<int>> solution(vector<vector<int>> arr1, vector<vector<int>> arr2) {
int row1 = arr1.size(), col1 = arr1[0].size(); // = row2
int col2 = arr2[0].size();
vector<vector<int>> answer(row1, vector<int>(col2, 0));
for(int k = 0; k<col1; k++){
for(int i = 0; i<row1; i++){
int temp = arr1[i][k];
for(int j = 0; j<col2; j++){
answer[i][j] += temp * arr2[k][j];
}
}
}
return answer;
}
빠른 거듭제곱 : O(log(exp))
long long fast_power(long long base, long long exp){
long long answer = 1; // 연산의 identity
while(exp){
if(exp & 1){ // exp % 2 == 1
answer *= base;
}
base *= base; // base = base * base
exp >>= 1; // exp = exp / 2
}
return answer;
}
행렬의 빠른 거듭제곱 : O(log(exp))
주의할 점은 result를 identity matrix로 잡고 시작해야 한다는 것!
typedef vector<vector<int>> matrix;
int MOD = 1000000007; // 나눌 값
// return result of matrix a * matrix b
// 성능을 위해 kij 순서로 곱
matrix operator*(const matrix& a, const matrix& b){
int ar = a.size(), bc = b[0].size(), acbr = b.size();
matrix result(ar, vector<int>(bc, 0));
for(int k = 0; k<acbr; k++){
for(int i = 0; i<ar; i++){
int temp = a[i][k];
for(int j = 0; j<bc; j++){
result[i][j] = (temp * b[k][j] + result[i][j]) % MOD;
}
}
}
return result;
}
int main(){
...
matrix base; cin>>base; // 행렬의 입력은 2중 for loop로 입력받겠지만, 편의상 이렇게 표현했다.
long long factor; cin>>factor; // 몇 번 제곱할 것인지
matrix result = MATRIX_IDENTITY; // 기본 수는 해당 연산의 identity로 설정
// 방법은 정수의 것과 동일하다.
while(factor != 0){
if(B & 1LL){
result = (result * m);
}
m = (m * m);
B >>= 1;
}
}
2진수에서 1의 개수 세기 (bit 연산)
int cntOne(int n){
int cnt = 0;
while(n){
cnt += (n & 1);
n = n >> 1;
}
return cnt;
}
진법 변환
아래처럼 10진수를 넘어가는 경우, 미리 digit string을 선언해 두고 나머지 값에 해당하는 값을 찾아오면 된다.
string toNotation(int number, int notation){
if(number == 0) return "0";
string digit = "0123456789ABCDEF";
string result = "";
while(number){
result = digit[number % notation] + result;
number /= notation;
}
return result;
}
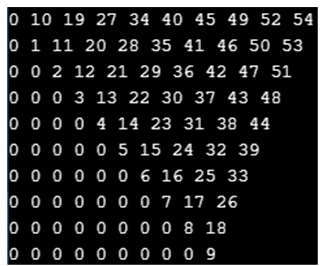
대각선 접근
아래와 같이 접근하면 대각선부터 우상단을 채워준다. i와 j의 차이를 d라고 두고, i를 기준으로 d를 계산하는 방식으로 접근하면 이해하기 쉽다.
for(int d = 0; i<len; d++) {
for(int i = 0; i<len-d; i++) {
int j = i + d;
DP[i][j] = k++;
}
}
좌표 압축 : O(nlogn)
vector의 정렬 후 중복 지우고 lower_bound로 mapper 값을 찾는 방법이다.
void gridCompress(vector<int> &arr){
vector<int> temp(arr.size());
for(int i = 0; i<arr.size(); i++){
temp[i] = arr[i];
}
sort(temp.begin(), temp.end());
temp.erase(unique(temp.begin(), temp.end()), temp.end());
for(int i = 0; i<arr.size(); i++){
arr[i] = lower_bound(temp.begin(), temp.end(), arr[i]) - temp.begin();
}
}
누적합 Prefix Sum
psum 배열의 제일 앞에 0을 두냐 마냐에 따라 indexing이 바뀌기 때문에 prefix sum을 구할 때 indexing에 주의하도록 하자.
1차원 Prefix Sum : 초기화 $O(n)$, 쿼리당 O(1)
range sum을 구할 때, start가 0이면 -1로 out of bound가 되어버리므로 start가 0일 때만 예외 처리를 해 주자.
// return partial sum
// psum[i] : sum from index 0 to index i
vector<int> setPsum(vector<int>& arr){
vector<int> psum(arr.size());
psum[0] = arr[0];
for(int i = 1; i<arr.size(); i++){
psum[i] = psum[i-1] + arr[i];
}
return psum;
}
// return range sum from index 'start' to index 'end'
int getRangeSum(vector<int>& psum, int start, int end){
if(start == 0) return psum[end];
return psum[end] - psum[start - 1];
}
int main(void) {
...
vector<int> psum = setPsum(arr);
int start, end;
cin>>start>>end;
cout<<getRangeSum(psum, start-1, end-1)<<'\n';
...
return 0;
}
2. 2차원 Prefix Sum : 초기화 $O(n^{2})$, 쿼리당 O(1)
// get partial sum from point (r1, c1) to point (r2, c2)
int getRangeSum(vector<vector<int>>& psum, int r1, int c1, int r2, int c2){
int result = psum[r2][c2];
if(r1 != 0) result -= psum[r1 - 1][c2];
if(c1 != 0) result -= psum[r2][c1 - 1];
if(r1 != 0 && c1 != 0) result += psum[r1 - 1][c1 - 1];
return result;
}
int main(void) {
...
int N, M; cin>>N>>M;
vector<vector<int>> board(N, vector<int>(N)), psum(N+1, vector<int>(N+1, 0));
// input
for(int i = 0; i<N; i++){
for(int j = 0; j<N; j++){
cin>>board[i][j];
}
}
// initialize prefix sum
// psum[r][c] : sum from (0, 0) to (r, c)
for(int r = 1; r<=N; r++){
for(int c = 1; c<=N; c++){
psum[r][c] = board[r-1][c-1] + psum[r-1][c] + psum[r][c-1] - psum[r-1][c-1];
}
}
int x1, y1, x2, y2;
while(M--){
cin>>x1>>y1>>x2>>y2;
cout<<getRangeSum(psum, x1, y1, x2, y2)<<'\n';
}
return 0;
}
순열, 조합, 중복순열, 중복조합
순열 Permutation : O(nPr)
// nPr의 경우
// arr : 순열할 원소, size n
// visited[i] : arr[i]가 방문되었는지 여부, 초기값 false, size n
// result : 순열 결과, size r
void permutation(int depth, int r, vector<int>& arr, vector<bool>& visited, vector<int>& result){
if(depth == r){
for(int i : result){
cout<<i<<" ";
}cout<<endl;
return;
}
for(int i = 0; i<arr.size(); i++){
if(!visited[i]){ // 사용된 것이라면 사용하면 안됨
visited[i] = true;
result[depth] = arr[i];
permutation(depth+1, r, arr, visited, result);
visited[i] = false;
}
}
}
// arr : 순열할 원소, size n
void permutation(vector<int>& arr){
sort(arr.begin(), arr.end());
do{
for(int i : arr){
cout<<i<<" ";
}cout<<endl;
}while(next_permutation(arr.begin(), arr.end()));
}
조합 Combination : O(nCr)
// nCr의 경우
// arr : 조합할 원소, size n
// result : 조합 결과, size r
void combination(int depth, int r, int prev_idx, vector<int>& arr, vector<int>& result){
if(depth == r){
for(int i : result){
cout<<i<<" ";
}cout<<endl;
return;
}
for(int i = prev_idx; i<arr.size(); i++){
result[depth] = arr[i];
combination(depth+1, r, i+1, arr, result);
}
}
// nCr, arr : 조합할 원소, size n
void combination(int n, int r, vector<int>& arr){
vector<int> temp(n, 0);
for(int i = 0; i<r; i++){
temp[i] = true;
}
do{
for(int i = 0; i<n; i++){
if(temp[i]) cout<<arr[i]<<" ";
} cout<<endl;
}while(prev_permutation(temp.begin(), temp.end()));
}
중복순열 Duplicated Permutation: O($_n \Pi _r$)
// nPIr의 경우
// arr : 순열할 원소, size n
// result : 순열 결과, size r
void duplicatePermutation(int depth, int r, vector<int>& arr, vector<int>& result){
if(depth == r){
for(int i : result){
cout<<i<<" ";
}cout<<endl;
return;
}
for(int i = 0; i<arr.size(); i++){
result[depth] = arr[i];
duplicatePermutation(depth+1, r, arr, result);
}
}
중복조합 Duplicated Combination : O(nHr)
// nHr의 경우
// arr : 조합할 원소, size n
// result : 조합 결과, size r
void duplicateCombination(int depth, int r, int prev_idx, vector<int>& arr, vector<int>& result){
if(depth == r){
for(int i : result){
cout<<i<<" ";
}cout<<endl;
return;
}
for(int i = prev_idx; i<arr.size(); i++){
result[depth] = arr[i];
duplicateCombination(depth+1, r, i, arr, result);
}
}
DFS로 순열/조합/중복순열/중복조합 탐색 시 요약
순열 : for문의 i는 depth에 상관없이 index 0부터, visited 사용 必
조합 : for문의 i는 이전 depth에서 뽑은 원소의 다음 index부터
중복순열 : for문의 i는 depth에 상관없이 index 0부터
중복조합 : for문의 i는 이전 depth에서 뽑은 원소의 index부터
Graph Algorithm
DFS : O(|V| + |E|)
procedure DFS(G)
for all vertex v in V do
visited[v] = false
end for
for visited[v] == false do
explore(v)
end for
procedure explore(w)
visited[w] = true
for each edge (w, u) in E do
if visited[u] == false then
explore(u)
end if
end for
BFS : O(|V| + |E|)
procedure BFS(G, s)
for all u in V do
dist(u) = INF
end for
dist(s) = 0 // visited[s] = true
Queue = [s] (queue containing just s)
while !Q.empty() do
u = Q.front()
for all edges (u, v) in E do
if dist(v) == INF then // unvisited
Q.push(v)
dist(v) = dist(u) + 1 // visited[u] = true
end if
end for
end while
다익스트라 Dijkstra : O((|V| + |E|) * log|V|)
struct mycomp{
bool operator()(pii&a, pii&b){
return a.second > b.second; // weight가 큰 것을 앞으로
}
};
// edges[i] : i가 edge의 시작인 edge list
// edges[i][0].first : edge list의 edge end
// edges[i][0].second : edge list의 edge weight
vector<int> dijkstra(int start, vector<vector<pii>> edges){
// dist initialize
vector<int> dist(V+1, INF);
dist[start] = 0;
// heap initialize
priority_queue<pii, vector<pii>, mycomp> pq;
pq.push({start, 0});
while(!pq.empty()){
int u = pq.top().first;
int u_weight = pq.top().second;
pq.pop();
// pq.top()에 연결된 모든 edge에 대해 dijkstra 수행
for(pii &edge : edges[u]){
int v = edge.first, v_weight = edge.second;
// 만약 갱신 가능하다면 dist 갱신 이후 pq에 다시 넣음
if(dist[v] > dist[u] + v_weight){
dist[v] = dist[u] + v_weight;
pq.push({v, dist[v]});
}
}
}
return dist;
}
벨만-포드 Bellman-Ford : O(|V| * |E|)
// edges[i] : i가 edge의 시작인 edge list
// edges[i][0].first : edge list의 edge end
// edges[i][0].second : edge list의 edge weight
vector<int> bellman_ford(int start, vector<vector<pii>> edges){
vector<long long> dist(V.size(), INF);
dist[start] = 0;
// V-1번 순회
for(int i = 0; i< V.size() - 1; i++){
// 모든 vertex에 대해
for(int v = 0; v < V.size(); v++){
// v의 모든 edge에 대해
for(pii edge : edges[v]){
int from = v, to = edge.first, weight = edge.second;
// dist[from]이 INF이면 갱신이 이상하게 될 수도 있음
if(dist[from] == INF) continue;
dist[to] = min(dist[to], dist[from] + edge.second);
}
}
}
bool hasNegCycle = false;
for(int v = 0; v < V.size(); v++){
for(pii edge : edges[v]){
int from = v, to = edge.first, weight = edge.second;
if(dist[from] == INF) continue;
if(dist[to] > dist[from] + weight){
hasNegCycle = true;
break;
}
}
}
if(hasNegCycle) return {-1};
else return dist;
}
플로이드-와샬 Floyd-Warshall : O(|V|³)
vector<int> V; // V는 vertex vector
vector<vector<int>> dist(V.size(), vector<int>(V.size(), INF)); // dist[i][j] : distance of vertex i to vertex j
for(int i = 0; i<V.size(); i++){
dist[i][i] = 0;
}
for(int temp = 0; temp < V.size(); temp++){
for(int from = 0; from < V.size(); from++){
for(int to = 0; to < V.size(); to++){
dist[from][to] = min(dist[from][temp] + dist[temp][to], dist[from][to]);
}
}
}
Dijkstra vs Bellman-Ford vs Floyd-Warshall
|
dijkstra
|
bellman-ford
|
floyd-warshall
|
|
한 점부터 다른 모든 점까지
|
한 점부터 다른 모든 점까지
|
모든 점부터 다른 모든 점까지
|
|
negative weight edge가 있을 시 사용 불가
|
negative weight edge가 있어도 사용 가능
negative weight cycle이 있으면 사용 불가
|
|
|
O((|V| + |E|) * log|V|)
|
O(|V| * |E|)
|
O(|V|³)
|
유니온-파인드 Union-Find (서로소 집합 Disjoint Set) : 1번의 연산에 O(log*n)
유의할 점, c++에서 find와 union, parent과 rank 이미 사용되고 있는 함수/변수이므로 앞의 것을 대문자로 바꿔 사용하자.
int Parent[1000001];
int Rank[1000001];
void Makeset(int s){
Parent[s] = s;
Rank[s] = 0;
return;
}
int Find(int x){
if(x == Parent[x]) return x;
Parent[x] = Find(Parent[x]); // x의 parent를 x의 root로 설정
return Parent[x];
}
void Union(int x, int y){
int rx = Find(x);
int ry = Find(y);
if(rx == ry) return;
if(Rank[rx] < Rank[ry]) // ry의 height가 더 크면 rx가 밑으로 글어가야 함
Parent[rx] = ry;
else{ // 그렇지 않다면 ry가 밑으로 들어가야 함
Parent[ry] = rx;
if(Rank[rx] == Rank[ry]){ // rank가 같으면 rank 조절
Rank[rx]++;
}
}
}
최소 신장 트리 Minimum Spanning Tree
Kruskal : O(ElogE)
Struct Edge{
int from, to, weight;
}
int Parent[1000001];
int Rank[1000001];
// union-find의 함수들
void Makeset(int s) {...}
int Find(int x) {...}
void Union(int x, int y) {...}
void Kruskal(vector<Edge> edges){
vector<Edge> MST;
sort(edges.begin(), edges.end()); // edge 정렬
for(Edge e: edges){ // 모든 edge에 대해
if(Find(e.from) != Find(e.to)){ // cycle 형성하지 않으면 MST에 push
MST.push_back(e);
Union(edge.from, edge.to); // Union 연산
}
}
}
Prim : O(ElogV)
struct cmp{
bool operator()(pii &a, pii &b){
return a.second > b.second;
}
};
// edges[i] : i가 edge의 시작인 edge list
// edges[i][0].first : edge list의 edge end
// edges[i][0].second : edge list의 edge weight
int Prim(vector<vector<pii>> edges){
int cost = 0;
set<int> MST;
priority_queue<pii, vector<pii>, pqcmp> pq; // pii.first : edge end, pii.second : edge weight
// 시작 vertex
MST.insert(0);
for(pii p : adjacent[0]){
pq.push(p);
} // 시작 vertex와 연결된 모든 edge를 pq에 넣는다.
while(MST.size() < V.size()){ // MST size가 |V|이 될 때까지 반복
pii p = pq.top(); pq.pop();
if(MST.find(p.first) == MST.end()){ // 연결되지 않았다면 연결
MST.insert(p.first);
cost += p.second;
for(pii next_edges : edges[p.first]){
pq.push(next_edges);
}
}
}
return cost;
}
트리 순회 Tree Traversal : O(V + E)
void preorder(node* cur_node){
if(cur_node == NULL) return;
cout<<cur_node->num<<endl;
result.push_back(cur_node->num);
preorder(cur_node->left, result);
preorder(cur_node->right, result);
}
void inorder(node* cur_node){
if(cur_node == NULL) return;
inorder(cur_node->left, result);
cout<<cur_node->num<<endl;
inorder(cur_node->right, result);
return;
}
void postorder(node* cur_node){
if(cur_node == NULL) return;
postorder(cur_node->left, result);
postorder(cur_node->right, result);
cout<<cur_node->num<<endl;
return;
}
위상 정렬 Topological Sort
// edges[i] : vertex i와 연결된 edge list
// num_incoming_edge[i] : vertex i로 들어오는 edge 개수
void topological_sort(vector<vector<int>>& edges, vector<int>& num_incoming_edge){
queue<int> q;
for(int i = 0; i <= V.size(); i++){ // 모든 vertex에 대해 incoming edge가 0인 것은 q에 push
if(num_incoming_edge[i] == 0) q.push(i);
}
bool isCycle = false;
vector<int> result;
for(int i = 0; i <= V.size(); i++){
if(q.empty()){
isCycle = true;
break;
}
int front = q.front(); q.pop();
result.push_back(front);
for(int adjacent : edges[front]){
num_incoming_edge[adjacent]--;
if(num_incoming_edge[adjacent] == 0) q.push(adjacent);
}
}
if(isCycle){
cout<<"this graph includes cycle!"<<endl;
return;
}
else{
for(int i = 0; i<result.size(); i++){
cout<<result[i]<<endl;
}
}
return;
}
'PS > Tips' 카테고리의 다른 글
| 알고리즘 하면서 공부해야 할 것들 & 고쳐야 할 것들 & 알면 좋은 것들 ** TODO (0) | 2022.06.24 |
|---|---|
| 나중에 다시 풀어 볼 문제들 (0) | 2022.06.24 |
| PS 하면서 알면 좋은 STL들 (0) | 2022.06.24 |
| PS 하면서 알면 좋은 SQL들 (0) | 2022.06.24 |
