Leetcode 1444. Number of Ways of Cutting a Pizza
문제를 보고, 일단 recursion dp 문제임을 깨닫고 dp로 해결하려 했다.
- dp[i][j][k] = 좌표 i, j에서 k번 cutting할 수 있는 개수라고 정의했다.
- 그러면 각 탐색 시 i, j, k에 대해 탐색하고, memoization을 사용하면 된다. 또, 각 탐색 시 i, j에 대해 [row로 쪼갤지, col로 쪼갤지]를 결정해야 한다. 그래서 [쪼갤 수 있는지 여부]를 판단하는 로직을 작성해야 한다.
- 그러나 [i, j]부터 [m, n]까지 전부 다 뒤지면서 경우의 수를 본다면 row 개수 m에 대해 mn 전체 순회해야 하고, col 개수 n에 대해 mn 전체를 순회해야 하므로 각 탐색에서 mn(m+n)이 걸린다. 시간 초과가 날 것이 뻔하다.
- 다른 접근이 필요했다. prefix sum을 이용해 [i, j]부터 [m, n]까지 prefix sum에 있는 row를 전부 합치고, col로 나눌 수 있는지 판단하고 / col을 전부 합치고, row로 나눌 수 있는지 판단하려 했다. 그러나 이 방법도 같은 이유로 불가.
어떻게 풀지? ... 고민하다 solution을 봤다. solution 미친 접근을 제시한다.
- [0, 0]부터 [m, n]까지의 prefix sum이 아니라, [m, n]부터 [0, 0]까지의 prefix sum을 이용해 쉽게 풀 수 있단다.
- 확실히 이렇게 하면 psum[r, c]가 [m, n]부터 [r, c]까지의 prefix sum이므로
- row를 자를 수 있을지 판단할 때는 psum[r][c] - psum[i][c]를 하면 column c에서 i번째 row를 잘랐을 때 apple 개수를 볼 수 있다.
- col을 자를 수 있을지 판단할 때는 psum[r][c] - psum[r][j]를 하면 row r에서 j번째 col을 잘랐을 때 apple 개수를 볼 수 있다.
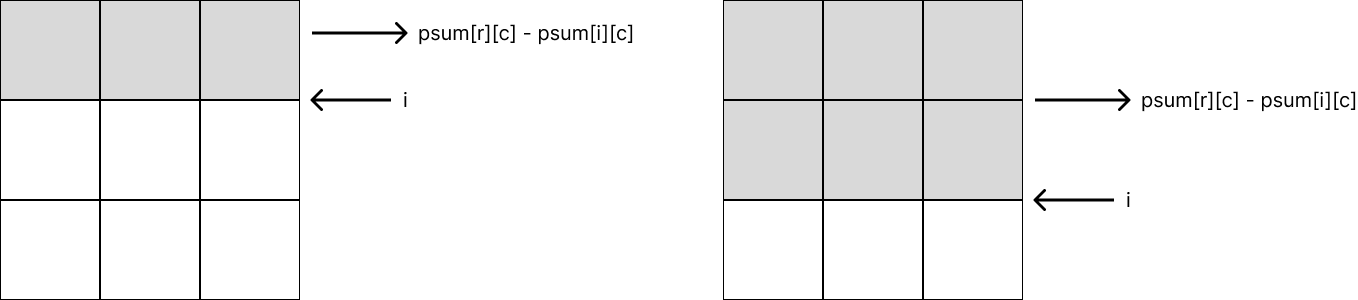
말로 하니까 조금 어려운데, 위 그림을 보자. row를 자르는 경우의 예시이다.
psum[r][c] - psum[i][c]는 어떤 i의 row를 자를 때, 그 위에 있는 apple의 개수이다. 이렇게 나타낼 수 있는 이유는 psum[r][c] 가 [m, n]부터 [r, c]까지 apple 개수이기 때문.
같은 방법으로 col도 똑같이 표현한다.
...아니 이걸 대체 어떻게 생각함? ... 진짜 ㅋㅋ
이걸 안다면 [쪼갤 수 있는지 여부]를 O(m+n)만에 판단할 수 있다. 그러면! DP해버리면 된다.
단, DP 종료조건은
- 해당 조각에 apple 개수가 0개여서 쪼갤 수 없거나 - 이게 젤 중요하다. 이 조건이 제일 먼저 와야 한다.
- 이 조건이 들어왔다는 거 자체가 더 이상 쪼갤 수 없는데 쪼개진 경우이기 때문.
- k == 0이어서 더 이상 쪼갤 필요가 없거나
- memoization이 되어 있거나
// Runtime 13 ms Beats 91.88%
// Memory 7.5 MB Beats 94.50%
typedef long long ll;
ll MOD = 1e9 + 7;
int psum[51][51];
int dp[51][51][11];
class Solution {
public:
int maxr, maxc;
int DFS(int r, int c, int k){
if(psum[r][c] == 0) return 0; // *** 생각하지 못함.
if(k == 0) return 1;
if(dp[r][c][k] != -1) return dp[r][c][k];
ll cnt = 0;
// row를 자를 수 있는지 판단
for(int i = r+1; i<maxr; i++){
if(psum[r][c] - psum[i][c] > 0){
cnt = (cnt + DFS(i, c, k-1)) % MOD;
}
}
// col을 자를 수 있는지 판단
for(int j = c+1; j<maxc; j++){
if(psum[r][c] - psum[r][j] > 0){
cnt = (cnt + DFS(r, j, k-1)) % MOD;
}
}
dp[r][c][k] = cnt;
return cnt;
}
int ways(vector<string>& pizza, int k) {
// dp 초기화
maxr = pizza.size(); maxc = pizza[0].size();
for(int i = 0; i<maxr; i++){
for(int j = 0; j<maxc; j++){
for(int m = 0; m<k; m++){
dp[i][j][m] = -1;
}
}
}
// trick : [0, 0]부터 [m, n]까지 하면 왼쪽 위에서 자른 결과가 후에 반영되지 않음.
// 따라서 [m, n]부터 [0, 0]까지 prefix sum 구함.
// 2차원 prefix sum 값 설정
for(int i = 0; i<=maxr; i++){
for(int j = 0; j<=maxc; j++){
psum[i][j] = 0;
}
}
for(int i = maxr-1; i>=0; i--){
for(int j = maxc-1; j>=0; j--){
psum[i][j] += psum[i+1][j] + psum[i][j+1] - psum[i+1][j+1] + (pizza[i][j] == 'A');
}
}
// dp[i][j][k] : 좌표 i, j를 k번 cutting해야 할 때 경우의 수
return DFS(0, 0, k-1); // *** 실수 : 주어진 k는 조각의 개수. 따라서 k-1을 넣어야 함
}
};
시간복잡도
O(mnk(m+n)이다. 전체 dp를 다 채워야 하니 O(mnk)가 걸리고, 각 dp 시 [row를 자를 수 있는지 / col을 자를 수 있는지] 여부를 판단하기 위해 O(m), O(n)을 사용한다. 따라서 각 탐색 시 O(m + n)이므로 전체 O(mnk(m+n))이다.
공간복잡도
함수 스택은 최대 O(k)만큼 쌓인다. 배열 할당에 O(mn), O(mnk)만큼 사용하므로 O(mnk)이다.
후기
미친 문제다. 접근은 거의 다 맞았는데, prefix sum을 뒤집는다는 생각은 전혀 하지도 못했다. 말도 안되는 trick이다. 담에 또 풀어봐야지.
'PS > PS Log' 카테고리의 다른 글
| 23.04.02. 풀었던 문제들 (0) | 2023.04.02 |
|---|---|
| 23.04.01. 풀었던 문제들 (0) | 2023.04.02 |
| 23.03.30. 풀었던 문제들 (0) | 2023.03.30 |
| 23.03.29. 풀었던 문제들 (0) | 2023.03.29 |
| 23.03.28. 풀었던 문제들 (0) | 2023.03.28 |
