이 글은 포스텍 김종 교수님의 컴퓨터SW시스템개론(CSED211) 강의를 기반으로 재구성한 것입니다.
이 글은 cache에 대해 다룬다.
Locality
locality는 프로그램이 최근에 참조한 주소와 그 근처의 주소에 반복적으로 참조하는 경향이다. temporal locality와 spatial locality 2종류가 있다.
- temporal locality : 최근에 참조된 주소를 반복적으로 참조하는 것을 의미한다.
- spatial locality : 최근에 참조한 주소 근처의 주소를 참조하는 것을 의미한다.
int sum = 0;
for(int i = 0; i<n; i++){
sum += a[i];
}
return sum;위와 같은 코드가 있다고 하자. 이 코드는 locality를 가지고 있다.
- 메모리(데이터) 측면에서
- 같은 변수 sum을 계속 참조한다. (temporal locality)
- stride-1 pattern을 가지면서 array a를 참조한다. (spatial locality)
- instruction 측면에서
- loop가 있는 경우 같은 instruction을 실행한다. (temporal locality)
- spatial locality : instruction은 항상 순서대로 실행된다. (spatial locality)
여기서 stride-n pattern이란 array의 n번째 element마다 참조하는 것을 의미한다.
Cache
Memory Hierarchy

cache에 대한 내용을 보기 전에, 메모리의 계층구조에 대해 짚고 넘어가야 한다. CPU는 속도가 굉장히 빠른 register를 직접 사용할 수 있지만 register는 비싼 만큼 한 컴퓨터에 그렇게 많이 넣을 수가 없다. register가 부족할 때 L1 cache를, L21cache가 부족할 때 L2 cache를, ... 이렇게 상위 계층 메모리가 부족할 때 하위 계층 메모리를 사용해 나간다.
Cache의 개념
cache는 level k의 memory를 level k+1 memory의 임시 저장소처럼 작동시켜 데이터에 더 빨리 접근할 수 있는 기법이며, locality와 memory hierarchy 때문에 작동한다.
- 크기가 작고 빠른 level k의 memory를 크기가 크고 느린 evel k+1 memory의 임시 저장소처럼 작동시킴으로써 느린 level k+1의 memory 대신 level k의 memory처럼 사용할 수 있다.
- locality에 의해 level k+1의 memory에서 한 번 참조했던 주소나 그 주소의 근처값이 참조될 가능성이 크므로 이 값들을을 미리 level k에 저장함으로써 level k의 memory처럼 사용할 수 있다.

일반적으로 main memory, local storage disk, remote secondary disk까지 cache를 사용하지는 않고 속도가 빠른 SRAM 정도만 cache로 사용한다. 또한 cache는 하드웨어가 직접 관리하며 어떠한 값을 메모리에서 찾을 때는 L1, L2, L3 cache를 먼저 찾은 뒤 없다면 main memory를 뒤진다.
Cache의 작동 방식
어떤 프로그램이 level k+1의 어떤 주소에 있는 정보 d를 필요로 할 때, level k의 cache를 먼저 살핀다.
Cache Hit
만약 level k의 cache에 d가 있다면 level k에서 그 값을 가져온다. 이 경우를 cache hit라고 하며, level k+1 대신 level k에서 가져오므로 당연히 더 빠르다.
Cache Miss
반면 level k의 cache에서 d를 찾지 못했을 때를 cache miss라고 한다. cache miss가 난다면 locality에 의한 다음 접근을 대비하기 위해 level k+1으로부터 d의 주소 주변에 있는 값들을 한 번에 가져온다. 이 때, cache가 꽉 찬 상태라면 덮어쓰며 이를 eviction이라 한다.
cache miss의 종류에는 크게 3가지가 있다.
- cold miss : cache가 비어있는 경우. 첫 번째 참조일 때 발생한다.
- capacity miss : d가 cache의 크기보다 더 큰 경우.
- conflict miss : cache의 크기는 충분한데도 eviction이 계속 발생해 miss가 계속 발생하는 경우
Cache의 구조

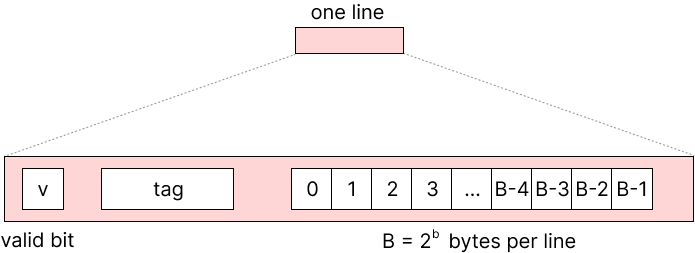

cache는 위 그림과 같이 이루어져 있다. address가 M(=2$^m$)개의 bit로 이루어진다고 가정하자.
cache는 총 S(=2$^s$)개의 set으로 이뤄지며, 각 set은 E(=2$^e$)개의 line으로 이루어져 있다. 하나의 line은 v bit + tag bit + B(=2$^b$)개의 block으로 구성되어 있으며, 하나의 block은 1 byte의 정보를 담는다. 이 때 v는 해당 cache가 valid한지 여부이며, tag는 cache line의 식별자이다. 따라서 total cache size = S * E * B = 2$^{s+e+b}$이다.
Cache Read
address를 tag / set index / block offset으로 크게 3부분으로 나누며 이를 통해 cache에 접근한다.
- set index bit를 이용해 cache set에 접근한다.
- set에 있는 모든 line에 대해 tag bit를 비교한다.
- 모든 line에 대해 tag bit가 일치하는 line이 없는 경우 cache miss이다.
- 있는 경우 valid bit가 1인지 살펴본다.
- not valid라면 cache miss이다.
- valid라면 cache hit이다. block offset을 이용해 line에 있는 block에 접근한다.
만약 cache miss가 났다면 바로 아래 level cache, 또는 main memory에서 값을 가져와 쓴다.
값을 가져와 쓸 때, cache set의 판정을 set index bit를 이용하기 때문에 set의 모든 line이 가득 찬 상태일 수도 있다. 이 경우 eviction이 일어나며 제일 적게 사용한 line을 교체하는 Least-Frequently-Used나 사용한 지 제일 오래된 line을 교체하는 Least-Recently-Used 등 다양한 정책을 사용해 cache를 교체한다.
Cache의 종류
- direct mapped cache : E = 1인 경우. 각 set당 1개의 line만 존재한다.
- E-way set associative cache : 1개의 set에 line이 E개인 경우.
Cache Write
cache read하는 방법을 살펴봤다. cache는 low hierarchy memory의 값을 high hierarchy memory로 복사하는 방식이라고 했다. 즉슨 memory, L2 cache, L1 cache 등 데이터의 사본이 많이 존재하는 상황인 것이다. 이 때 *a = 10;과 같이 원래 있던 메모리의 값을 수정하는 경우는 어떻게 해야 할까?
write도 read와 같은 방식으로 일단 cache에 접근한다. 이후 write hit냐, write miss냐에 따라, 그리고 선택에 따라 값을 업데이트하는 방식이 달라진다.
- write hit : 해당 주소가 cache에 있는 경우
- write through : 바꾼 값을 바로 memory에 저장한다.
- write back : cache가 eviction될 때만 memory에 저장한다. 단, 이 경우 수정되었는지 여부를 나타내는 dirty bit를 모든 line에 추가해야 한다.
- write miss : 해당 주소가 cache에 없는 경우
- write allocate : write하려는 block을 cache로 가져온 뒤 cache의 값을 수정한다. (이 경우 write back이 일어날 것이다.)
- no write allocate : 바꾼 값을 바로 memory에 저장한다.
middle bit를 set index로 사용하는 이유

address를 쪼갤 때 block offset은 spatial locality를 위해 참조한 address의 주변에 있는 값들을 가져오기 위해 필요하다. 주변에 있다는 것은 bit가 인접해 있다는 말이므로 block offset은 LSB부터 시작하는 것이 맞는 것 같다.
그렇다면 set index bit가 가운데 있어야 할 필요가 있을까? tag bit와 위치가 바뀌어도 되지 않을까? 그렇지 않다. set index bit는 중간 위치인 block offset bit 다음으로 오는 것이 좋다. 그 이유를 예시와 함께 보자.

예시니까 조금 단위를 줄여 보자. address는 6byte이고 16byte의 directed mapped cache가 있다고 하자. tag bit, set index bit, block offset bit 모두 각각 2bit씩이라고 두자. 그러면 다음과 같은 상황이 된다.

자.. 그러면 set index가 제일 앞에 오는 상황이라 치자. 그러면 어떤 순서로 cache에 저장될까?
set index가 MSB부터 시작한다면 인접해 있는 memory block들이 같은 set에 들어가게 된다. 만약 cache line의 개수가 set의 개수보다 더 크다면 상관없겠지만 보통은 그렇지 않다. 인접한 memory address들이 같은 set에 들어가게 되면 eviction이 계속 일어나기 때문에 spatial locality를 잘 살릴 수 없게 된다.
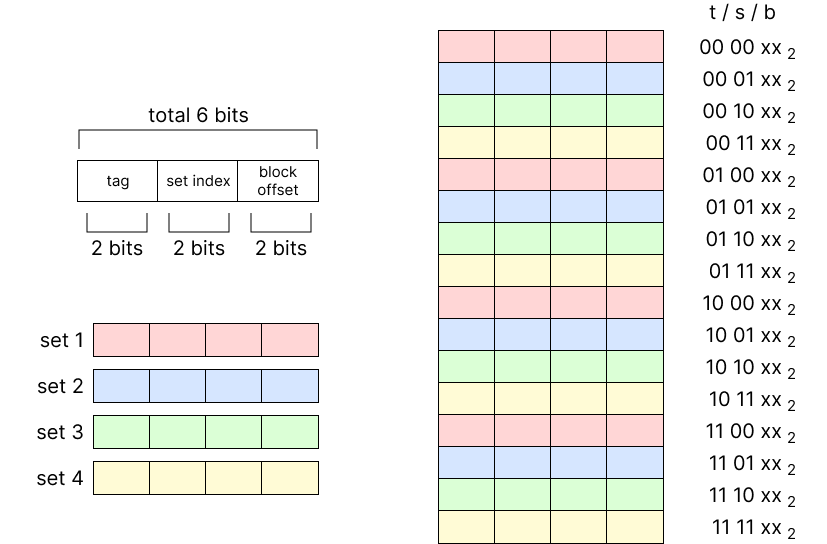
반면 set index가 중간에 있는 상황이라면 어떤 순서로 cache에 저장될까?
위와 같이 인접해 있는 memory block들이 각기 다른 set에 들어가게 되므로 연속된 memory block이 모두 cache에 저장된다. 위 예시에서는 0000xx$_2$부터 0011xx$_2$까지 연속된 memory block이 set 1부터 set 4까지 고르게 caching된다. 따라서 인접한 memory address가 모두 cache에 있기 때문에 spatial locality를 잘 활용할 수 있게 된다.
Cache Performance
- miss rate : # of misses / # of references.
- L1 cache의 경우 보통 3~10% 정도이며 L2 cache의 경우 크기에 따라 천차만별이다.
- hit rate : # of hits / # of references = 1 - miss rate.
- hit rate 대신 miss rate를 사용한다. hit rate 99%와 97%는 약 2배 차이가 나기 때문.
- hit time : cache 안의 line을 CPU로 전달하는 데 걸리는 시간.
- 보통 L1 cache의 경우 약 4 clock, L2 cache의 경우 약 10 clock정도가 걸린다.
- miss panelty : cache miss로 인해 더 필요한 시간
- 보통 50 ~ 200 clock정도이다.
hit rate 99%와 97%의 성능 비교를 보자. 비관적으로 생각해 hit time을 4clock, miss penalty를 200clock이라 둬 보자. 97% hit의 경우 100번의 cache 참조가 있을 때 4clock * 100 + 200clock * 3 = 1000 clock이다. 반면 99% hit의 경우 4clock * 100 + 200clock * 1 = 600 clock이다. 약 2배의 시간이 걸리는 셈.
Cache-Friendly Code
tag bit와 set index가 같은 주소들은 모두 같은 cache에 들어가므로 array에 접근할 때는 stride-1 pattern을 유지하는 것이 spatial locality 향상에 좋고, 같은 메모리에 반복접근하기보다는 변수를 하나 만드는 것이 temporal locality 향상에 좋다.
행렬곱 알고리즘 포스팅에서 cache를 고려한 행렬곱 알고리즘을 다룬적이 있었다. 여기서 사용한 기법이 바로 cache-friendly, 즉 stride-1 pattern + 같은 메모리에 반복접근 대신 local variable을 쓰는 방향으로 작성한 것이다.
먼저 일반적은 행렬곱 예시를 보자. n by n size인 arr1과 arr2의 행렬곱 결과를 result에 저장할 것이며 cache에 4개의 element가 들어가고 n > 4라 가정하자.
제일 첫 접근 : ijk
for(int i =0; i<n; i++){
for(int j = 0; j<n; j++){
result[i][j] = 0;
for(int k = 0; k<n; k++){
result[i][j] += arr1[i][k] * arr2[k][j];
}
}
}보통이라면 위와 같이 3중 for문을 머리에서 받아들이기 쉬운 ijk 순서로 작성할 것이다. 여기서 result[i][j]에 계속 접근하므로 result 배열이 계속 caching될 것이다. result에 접근하는 대신 local variable을 사용하면 register에 계속 값이 남아 있으므로 좀 더 빨라질 것이다.
개선 1 : ijk + local variable 사용
for(int i =0; i<n; i++){
for(int j = 0; j<n; j++){
int temp = 0;
for(int k = 0; k<n; k++){
temp += arr1[i][k] * arr2[k][j];
}
result[i][j] = temp;
}
}자. 이제 각각의 matrix arr1, arr2, result가 어떤 패턴으로 접근하는지 생각해 보자. 제일 안쪽의 loop에서 arr1은 stride-1 pattern으로, arr2는 stride-j pattern으로, result는 하나의 element에만 접근한다.
miss rate를 계산해 보자. arr1의 경우 stride-1 pattern이므로 연속된 배열의 값들이 캐싱되므로 miss rate는 0.25이다. arr2의 경우 stride-j pattern에 n>4이므로 miss rate는 1이다. result의 경우 고정된 값에 접근하므로 항상 캐싱되어있다. 따라서 total miss rate = 1.25이다.
변형 1 : jki + local variable 사용
for(int j = 0; j<n; j++){
for(int k = 0; k<n; k++){
int temp = arr2[k][j];
for(int i = 0; i<n; i++){
result[i][j] += arr1[i][k] + temp;
}
}
}jki 순서로 바꾸면 코드는 위와 같다. 제일 안쪽의 loop에서 arr1은 stride-k pattern으로, arr2는 하나의 element로 고정, result는 stride-j pattern이다.
miss rate를 계산해 보자. arr1은 stride-k pattern에 n>4이므로 miss rate는 1이다. arr2는 local variable에 접근하므로 항상 캐싱되어있다고 생각할 수 있고, arr2는 stride-j pattern에 n>4이므로 miss rate는 1이다. 따라서 total miss rate = 2이다. ijk의 경우보다 더 나쁜 상황이 되었다.
개선 2 : kij + local variable 사용
for(int k = 0; k<n; k++){
for(int i = 0; i<n; i++){
int temp = arr1[i][k];
for(int j = 0; j<n; j++){
result[i][j] += temp * arr2[k][j];
}
}
}kij 순서로 바꾸면 코드는 위와 같다. 제일 안쪽의 loop에서 arr1은 하나의 element로 고정(local variable), arr2는 stride-1 pattern, result도 stride-1 pattern이다.
miss rate를 계산해 보자. stride-1 pattern인 arr2와 result의 경우 연속된 값이 캐싱되므로 miss rate = 0.25, arr1은 local variable에 접근하므로 항상 캐싱되어있다고 생각할 수 있으므로 miss rate = 0. 따라서 total miss rate = 0.5이다. 3중 for문으로 cache를 고려해 빠르게 계산할 수 있다.
잘못된 내용이나 지적, 오탈자 등은 언제나 환영합니다.
'CS > OS' 카테고리의 다른 글
| [컴퓨터 SW] Exceptional Control Flow & Process (0) | 2023.06.19 |
|---|---|
| [컴퓨터 SW] Static Linking (0) | 2023.06.17 |
| [컴퓨터 SW] Storage - RAM & Disk (0) | 2023.06.14 |
| [컴퓨터 SW] Buffer Overflow (0) | 2023.06.11 |
| [컴퓨터 SW] Array/Structure/Union의 할당과 접근 (0) | 2023.06.11 |
![[컴퓨터 SW] Cache와 Locality](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FQvJ8n%2FbtsjYqZ66JN%2FMs1OhMZLBOE466bsKYLGjk%2Fimg.png)