이 글은 포스텍 김종 교수님의 컴퓨터SW시스템개론(CSED211) 강의를 기반으로 재구성한 것입니다.
이 글에서는 컴퓨터가 정보를 표현하는 방식인 bit와 연산에 대해 알아본다.
Bit와 Bytes
컴퓨터는 모든 정보를 0과 1로 표현하며, 표현의 최소 단위를 하나의 bit라고 정의한다. byte는 8개의 bit로 구성되어 있으며 0과 1로 이루어진 수가 8자리로 이루어져 있으므로, 2진수로 숫자를 표현한다.
- 1byte == 8bit
- 1byte는 $00000000_2$부터 $11111111_2$까지 표현 가능하며, 10진수로는 0~255, 16진수로는 00$_{16}$부터 FF$_{16}$까지 표현할 수 있다.
일반적인 수들의 byte 개수는 다음과 같다.
| Data Type | 32bit | 64bit |
| char | 1 | 1 |
| short | 2 | 2 |
| int | 4 | 4 |
| long | 4 | 8 |
| float | 4 | 4 |
| double | 8 | 8 |
| pointer (address) | 4 | 8 |
Bit의 연산
and, or, not, xor, shift 크게 5개의 연산자가 있다.
AND, OR, NOT, XOR
| Operation | Expression | Meaning | Example |
| And | A & B | A와 B 둘 다 1이어야 1 | 01101001 & 01010101 = 01000001 |
| Or | A | B | A와 B 둘 중 하나라도 1이면 1 | 01101001 | 01010101 = 01111101 |
| Not | ~A | A의 반대 비트. 1이면 0, 0이면 1. | ~ 01010101 = 10101010 |
| Xor | A ^ B | A, B의 bit가 다르면 1 | 01101001 ^ 01010101 = 00111100 |
SHIFT
shift operation은 bit를 옮기는 것이다. 크게 left shift, right shitf가 있고, right shift의 경우 Logical shift, Arithmetic shift가 있다.
- left shift는 x << y로 표현하며, x를 왼쪽으로 y칸 당기며, 새로이 생기는 오른쪽 bit에는 0을 넣는다.
- right shit : x >> y로 표현하며, x를 오른쪽으로 y칸 당긴다.
- logical shift의 경우 새로 생기는 왼쪽 bit에는 0을 넣는다.
- arithmetic shift의 경우 새로 생기는 왼쪽 bit에는 기존에 제일 왼쪽에 있던 bit(Most Significant Bit - MSB)를 넣는다.
| x | 01100010 | | | x | 10100010 |
| x << 3 | 00010000 | | | ||
| Log. x >> 2 | 00011000 새로 생기는 부분 0 넣음 |
| | Log. x >> 2 | 00101000 새로 생기는 부분 0 넣음 |
| Arith. x >> 2 | 00011000 MSB가 0이므로 0 넣음 |
| | Arith. x >> 2 | 11101000 MSB가 1이므로 1 넣음 |
Bit를 이용한 숫자의 표현 : Integer
integer는 정수형 데이터 타입이다. 데이터 타입이니만큼 integer 또한 bit로 표현되며, 모든 수가 그렇듯 2진수로 표현한다. 부호가 있는 signed int와 부호가 없는 unsigned int로 나눌 수 있다.
Unsigned Integer
부호가 없는 정수형 데이터 타입. 어떤 연속된 bit에 대해 다음 수식을 통해 부호 없는 정수로 바뀐다.
$\sum_{i=0}^{w-1} x_i2^i$
예를 들어 1011이라면 1 + 2 + 8 = 11로 변환된다. 따라서 bit 개수를 w라고 했을 때 최소값은 0, 최대값은 $2^w-1$이 된다.
일반적으로 unsigned int는 4byte, 즉 32bit이므로 2^32-1인 4,294,967,295가 최대값이다.
Signed Integer
부호가 있는 정수형 데이터 타입이다. 어떤 연속된 bit에 대해 다음 수식을 통해 부호 있는 정수로 바뀐다.
$-x_{w-1}2^{w-1} + \sum_{i=0}^{w-2} x_i2^i$
예를 들어 1011이라면 -8 + 1 + 2 = -5로 변환된다. 이 방식을 2의 보수(Two's Complement)라고 부르며, 제일 앞에 있는 bit인 MSB(Most Significant Bit)가 부호를 결정한다. MSB가 1이면 음수, 0이면 양수가 된다. 따라서 bit 개수를 w라고 했을 때 최소값은 $-2^{w-1}$, 최대값은 $2^{w-1} - 1$이 된다.
일반적으로 signed int는 4byte, 32bit이므로 최소값은 –2,147,483,648, 최대값은 2,147,483,647이다.
또, Two's Complement에서 아주 중요한 특징이 있으므로 외워두면 좋다.
~x + 1 = -x
~x + x은 항상 111...11이므로 ~x + x = -1이다.
따라서 ~x + 1 = -x
Signed와 Unsigned의 연산
signed value와 unsigned value가 섞여 있는 경우 explicit하게 명시하지 않는 이상 signed value가 unsigned value로 implicitly casting된다. casting 시 bit는 유지되지만 해석을 다르게 하는 방식으로 casting한다.
- 예를 들어 signed integer -5가 있다고 하자. 이를 unsigned로 casting한다면 bit는 $1011_2$로 유지되지만 unsigned로 해석하기 때문에 11로 연산한다.
- 이렇듯 unsigned에서 signed로 casting하는 경우 unsigned integer를 bit로 바꾸고, 해당 bit를 signed integer로 해석한다. 마찬가지로 signed에서 unsigned로 casting하는 경우 signed integer를 bit로 바꾸고, 해당 bit를 unsigned integer로 해석한다.
몇 가지 예시
C에서 signed, unsigned 연산을 한다고 치자. C에서 아무 값도 붙이지 않는다면 default로 signed값이 만들어지고, explicit하게 U를 붙여주면 unsigned로 만들어진다.
| 좌항 | 우항 | 비교값 | |
| 1 | 0 | 0U | == |
| 2 | -1 | 0 | < |
| 3 | -1 | 0U | > |
| 4 | 2147483647 | -2147483647 - 1 | > |
| 5 | 2147483647U | -2147483647 - 1 | < |
| 6 | -1 | -2 | > |
| 7 | (unsigned)-1 | -2 | > |
| 8 | 2147483647 | 2147483648U | < |
| 9 | 2147483647 | (signed)2147483648U | > |
- signed와 unsigned를 implicitly 비교하는 경우 unsigned로 casting된다. signed 0은 000.00, unsigned 0은 000..00이므로 동일하다. ==.
- signed와 signed를 비교하는 경우 signed로 비교한다. 따라서 <.
- unsigned로 casting. signed -1은 111...11, unsigned 0은 000...00이므로 >.
- 둘 다 signed이며 int min은 -2147483648이므로 overflow가 일어나지 않음. signed의 비교이므로 >.
- unsigned 2147483647은 0111..11이고, signed -2147483648은 100...00이다. unsigned의 비교이므로 <.
- signed의 비교이다. 따라서 >.
- signed -1은 111...11, signed -2는 111...10이다. 좌항이 unsigned로 casting했으므로 비교는 unsigned로 해야 한다. 따라서 >.
- signed 2147483647는 0111..11, unsigned 2147483648은 1000...00이다. unsigned의 비교이므로 <.
- signed 2147483647은 0111..11, unsigned 2147483648은 1000...00이다. 단, unsigned인 우항을 signed로 casting했으므로 signed의 비교가 된다. 0111..11은 2147483647, 1000..00은 -2147483648이므로 >.
Signed와 Unsigned의 Expanding, Truncating
expanding은 수의 범위를 늘이는 것이다. 예를 들어 short를 int로 형변환하는 것이 있다.
- expanding 시
- unsigned : 앞에 붙는 부분은 0을 붙인다.
- signed : 앞에 붙는 부분은 MSB와 같은 bit로 둔다.
| decimal | hexadecimal | binary | |
| sx (short s) | 15213 | 3B 6D | 00111011 01101101 |
| ix (integer x) | 15213 | 00 00 3B 6D | 00000000 00000000 00111011 01101101 |
| sy (short y) | -15213 | C4 93 | 110100100 10010011 |
| iy (integer y) | -15213 | FF FF C4 93 | 11111111 11111111 11000100 10010011 |
반대로 truncating은 수의 범위를 줄이는 것이다. 예를 들어 int를 short로 형변환하는 것이다.
- truncating 시에는 unsigned/signed 구분하지 않고 앞자리를 버리고 재해석한다.
- 예를 들어 unsigned 0x00010000을 2byte로 자른다면 unsigned 0x0000이 된다.
- signed 0x00011000 (10진수 24)을 2byte로 자른다면 signed 0x1000 (10진수 -8)이 된다.
Signed와 Unsigned의 사칙연산
1. Addition
unsigned든 signed든 bit-level의 동작은 동일하다. 둘 모두 bit로 환산하고, 더하고, 초과되는부분은 버린다. signed와 unsigned의 casting에서 bit는 유지되지만 해석은 다르게 하는 방식과 동일하게, [bit의 덧셈 - 올림된다면 해당 부분은 버림 - signed 또는 unsigned에 따라 해석]의 순서를 따른다.
- unsigned : 덧셈 시 overflow가 발생할 수 있다. unsigned의 경우 항상 0보다 크므로, overflow가 발생하는 경우 해당 수가 담을 수 있는 최대값을 초과하는 경우만 존재한다.
$UAdd_{w}(u, v) = \begin{cases}
u + v & \text{ if } u + v < 2^{w} \\
u + v - 2^w & \text{ if } 2^w \leq u + v
\end{cases}$
- signed : 덧셈 시 overflow가 발생할 수 있다. 음수 값 2개를 더해 해당 수의 최소값보다 더 작아질 수도 있고, 양수 값 2개를 더해 해당 수의 최대값보다 더 커질 수도 있다.
$TAdd_{w}(u, v) = \begin{cases}
u + v + 2^w & \text{ if } u + v < 2^{w-1} \text{ : Negative overflow}\\
u + v & \text{ if } -2^{w-1} \leq u + v < 2^{w-1} \text{ : normal case} \\
u + v - 2^w & \text{ if } 2^{w-1} \leq u + v \text{ : Positive overflow}
\end{cases}$
2. Multiplication
덧셈과 동일하게 unsigned든 signed든 상관없이 bit로 환산하고, 올림된다면 해당 부분은 버리고, signed 또는 unsigned에 따라 해석한다. 덧셈은 - 연산으로 초과분을 뺄 수 있지만 곱셈은 modular 연산으로 결과를 계산한다. (사실 덧셈도 modular 연산과 동일하긴 하다.)
$UMult_{w}(u, v) = TMult_{w}(u, v) = u \cdot v \text{ mod } 2^w$
2-1. Multiplication with Shift
shift는 bit를 옮기는 연산이다. <<는 무조건 왼쪽으로 한칸 당기는데, 이는 multiplication과 동일하며, 남는 bit는 버린다. 즉 곱셈 연산과 동일하다.
u << k == $u \cdot 2^{k}$
곱셈보다 shift 연산이 훨씬 빠르다. 이 특징을 이용해 shift 연산의 결과물을의 차를 이용해 곱셈 연산을 할 수도 있다.
u << 3 == 8u
u << 5 - u << 3 = 32u - 8u = 24u
2-2. Divide with Shift
<< 연산은 왼쪽으로 당기니 곱셈이다. 반대로, >> 연산은 오른쪽으로 당기니 나눗셈 연산이다. 단, 소수점 아래에 해당하는 bit들은 모두 버려지므로 소수점을 버리는 나눗셈 연산이라고 생각하면 된다.
unsigned의 경우 : u >> k = └u/k┘(소수점 버림 연산)
signed의 경우 : u >> k = $\begin{cases}
& └u/k┘ \text{ if } u \geq 0 & k > 0 \\
& ┌u/k┐ \text{ if } u < 0 & k > 0
\end{cases}$
음수를 표현할 때 -N + F 형태, 즉 [음의 정수 + (항상 양인) 소수] 형태로 값을 표현하기 때문에 u < 0이라면 올림해 주어야 한다.
예를 들어 signed 1001$_2$ (-7) /2 를 한다고 하자. -7 / 2 = -3이 나올 것이다. 그러나 >> 1로 shift 연산을 하면 1100.1$_2$ (-4 + 0.5)가 된다. 따라서 올림해 1101$_2$ (-3)으로 만들어 주는 것이다.
몇 가지 예시
x, y는 signed integer이고 ux와 uy는 unsigned integer이다.
| 문제 | 결과 | |
| 1 | x < 0 then ((x*2) < 0) | false |
| 2 | ux >= 0 | true |
| 3 | x & 7 == 7 then (x<<30) < 0 | true |
| 4 | ux > -1 | false |
| 5 | x > y then -x < -y | false |
| 6 | x * x >= 0 | false |
| 7 | x > 0 && y > 0 then x + y > 0 | false |
| 8 | x >= 0 then -x <= 0 | true |
| 9 | x <= 0 then -x >= 0 | false |
| 10 | (x | -x) >> 31 == -1 | false |
| 11 | ux >> 3 == ux / 8 | true |
| 12 | x >> 3 == x / 8 | false |
| 13 | x & (x-1) != 0 | false |
- signed x의 경우 overflow가 발생할 수 있다. overflow가 발생하면 양수가 될 수도 있다. false.
- signed 0은 000..00이고, 이를 unsigned와 비교하면 항상 true이다.
- x & 7 == 7이라는 의미는 x는 ???...111처럼 끝 3자리가 1이라는 뜻이다. 32bit를 기준으로 생각했을 때, 30칸 left shift를 하면 110000..00이 된다. 따라서 음수를 의미한다. true.
- -1은 bit로 표현하면 111...11이다. unsigned integer 중 최대값이 111...11이므로, 이 명제는 틀렸다. false.
- Two's complement의 성질에 의해 -x = ~x + 1이다. 동일하게 -y = ~y + 1이고, x > y일 때 ~x + 1과 ~y + 1을 비교하는 경우를 생각해 보면 된다. overflow가 나는 경우를 생각해 보자. 예를 들어 x = 0000$_2$이면 ~x + 1 = 0000$_2$, y = 1000$_2$이면 ~y + 1 = 1000$_2$이므로 ~x + 1 > ~y + 1이다. false.
- signed integer의 곱은 bit끼리 곱하고, overflow가 난 부분을 버린다. 남은 부분의 sign bit가 1이면 음수가 될 수 있다. false.
- signed integer 2개를 더했을 때 overflow가 발생할 수 있고, 따라서 음수가 될 수도 있다. false.
- Two's complement의 성질에 의해 -x = ~x + 1이다. signed integer인 x >= 0이라는 뜻은 sign bit가 0이라는 뜻이며, 0???..??로 이루어져 있다. 여기에 Not 연산을 취하면 1???...??가 되고, 여기에 1을 더하면 아래 2가지 경우가 생긴다.
- overflow가 나는 경우 000...00이 된다. 이 경우 0이다.
- overflow가 나지 않는 경우 sign bit는 1이다.
- 따라서 true.
- 바로 위 문제와 마찬가지로 Two's complement의 성질에 의해 -x = ~x + 1이다. signed integer x <= 0이라는 뜻은 x는 000..00이거나 sign bit가 1이라는 뜻이다. 여기에 1을 더하면 아래 2가지 경우가 생긴다.
- x가 000..00인 경우, ~x = 111..11, ~x + 1 = 000..00
- x의 sign bit가 1인 경우, x = 1??...??, ~x = 0??..??, ~x + 1은 0???..??이 될 수도 있지만, 1000..00이 될 수도 있다. 이 경우 -x < 0이므로 false.
- x = 1000$_2$인 경우를 생각해 보면 된다. ~x = 0111, ~x + 1 = 1000, signed 1000$_2$ = -8이다.
- x가 0000인 경우를 생각해 보자. x가 0000$_2$인 경우 -x = ~x + 1 = 0000$_2$므로 x | -x = 0000$_2$, 따라서 false.
- ux >> 3 == ux / 8이다. 정의에 의해 그렇다. true
- x >> 3에서, x >= 0이라면 └x/8┘, 즉 x/8이겠지만 x < 0이라면 ┌x/8┐으로 다른 값이 된다.
- signed x = 0000$_2$인 경우를 생각해 보자. 그러면 x - 1 = 1111$_2$이므로 0000$_2$ & 1111$_2$ = 0이다. false.
Bit를 이용한 숫자의 표현 : Floating Point
위에서 정수를 2진수로 표현하는 방식을 알아봤다. 그렇다면 소수는 어떻게 표현할까?
소수의 이진수 형식 표현
정수와 동일하게 소수점 아래에서도 2진수의 거듭제곱 형태로 표현한다.
$\sum_{}^{} b_k \times 2^{k}$
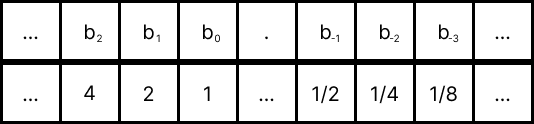
예를 들어 101.101이라면 4 + 1 + 1/2 + 1/8 = 5.625가 된다.
이론상 무한급수의 형태로 모든 소수를 표현할 수 있다. 그러나 컴퓨터의 저장공간은 무한하지 않기 때문에 적당히 근사해서 소수를 표현해야 한다.
IEEE Floating Point
그 방법이 바로 Floating Point다.
(-1)$^s$M2$^E$
위와 같이 byte를 3개의 부분으로 쪼개어 소수를 표현한다. 어려워 보이지만 단순하다. 화학 등에서 사용하는 유효숫자 개념을 2진수로 표현한 것이다.
- s : sign bit. signed integer와 동일하게 0이면 양수, 1이면 음수이다.
- M : significand(유효숫자). 일반적으로 [1.0, 2.0)의 범위를 가진다.
- E : exponent(승수). 2의 승수를 나타낸다.
예를 들어 22 = 10110$_2$이고, 이를 유효숫자 형식으로 표현하면 1.001$_2$ * 2$^4$로 표현한다.
이렇게 유효숫자 형식으로 소수를 표현한 이후sign bit s는 s에, significant M은 exp에, exponent E는 frac에 근사한다. 그러나 무한소수같은 경우에는 유효숫자가 무한하지만 메모리의 한계로 인해 적당한 근사값을 지정한다.

single precision(float)는 exp가 8bit, frac이 23bit이고 double precision(double)은 exp가 11bit, frac이 52bit이다.
encoding 될 때 E와 M이 부분이 encoding된다. exp의 값에 따라 floating point가 의미하는 값이 달라진다.
Case 1. Normalized value
exp != 000..00 && exp != 111..11인 경우. 일반적인 경우이다.
- bias = 2$^{k-1}$ -1. k는 exp bit의 개수이다.
- Exp = exp bit의 unsigned value
- E = Exp - bias
- single precision인 경우 k = 8이므로 bias = 127, Exp는 1부터 254까지의 값을 가지므로 E의 범위는 [-126, 127]이다.
- double precision인 경우 k = 11이므로 bias = 1023, Exp는 1부터 2046까지의 값을 가지므로 E의 범위는 [-1022, 1023]이다.
- M = 1.xxx..xx$_2$일 때, xxx..xx가 frac의 bit가 된다.
- 000..00일 때 최소값인 M = 1이 되고, 111..11일 때 최대값인 M = 2-ε이 된다.
Case 2. Denormalized Value
exp == 000..00인 경우. 0 또는 0에 가까운 수를 표현한다.
- bias = 2$^{k-1}$ -1. k는 exp bit의 개수이다.
- E = 1 - bias
- M = 0.xxx..xx$_2$일 때, xxx..xx가 frac의 bit가 된다.
- exp == 000..00 && frac == 000..00인 경우 : 0을 나타낸다. sign bit에 따라 +0 또는 -0이 된다.
- exp == 000..00 && frac != 000..00인 경우 : 0에 가까운 수를 표현한다.
Case 3. Special Value
exp == 111..11인 경우. INF 또는 NaN을 나타낸다.
- exp == 111..11 && frac == 000..00인 경우 : INF를 나타낸다. sign bit에 따라 +INF, -INF를 나타낼 수 있다. 일반적으로 overflow의 표현이며 0으로 나눌 때 INF로 간다.
- exp == 111..11 && frac != 000..00인 경우 : NaN을 나타낸다. sqrt(-1), INF - INF, INF * 0 등 숫자로 표현할 수 없는 경우를 나타낸다.
변환 방법
Floating Point to Number
- 수를 정해진 형식에 따라 sign bit, exp bit, frac bit로 분류한다.
- exp bit, frac bit을 이용해 normalized / denormalized / special 분류를 한다.
- exp bit로 E값을, frac bit로 M값을 구한다.
- (-1)$^s$M2$^E$에 값을 넣어 수를 구한다.
Number to Floating Point
- 수를 2진수의 급수 형태로 표현한다.
- (-1)$^s$M2$^E$ 형식으로 변환한다.
- 정해진 bit의 개수에 따라 bias를 구하고, E와 bias를 이용해 exp bit를 구한다. 이 때 rounding을 하며, overflow 발생 시 exp값을 조정한다.
- M값으로 frac bit를 구한다.
Rounding
앞서 (-1)$^s$M2$^E$ 형식으로 표현된 수를 sign bit s는 s에, significant M은 exp에, exponent E는 frac에 encoding한다. 그러나 컴퓨터의 메모리가 한정되어 있기 때문에 무한소수로 표현되는 M을 exp에 매핑시키려면 반올림해야 한다.
M이 1.BBGRXXX형태로 나타난다고 하자. G, R, S가 의미하는 것은 다음과 같다.
- G : guard bit, frac의 제일 작은 bit에 해당하는 값
- R : round bit라고 부르며, 지워질 첫 번째 bit이다.
- S : sticky bit라고 부르며, 나머지 bit들의 or 연산 값이다. 즉슨 하나라도 1이라면 S = 1이 된다.
반올림을 하는 조건은 크게 아래 2가지가 있다.
- R == 1 && S == 1
- 이 경우 guard bit 아래의 값이 guard bit의 절반보다 항상 더 크므로 올림한다.
- G == 1 && R == 1 && S == 0
- 이 경우 guard bit 아래의 값이 guard bit의 절반과 같지만 관습적으로 round-to-even을 적용해 짝수가 되는 쪽으로 올림을 해 준다.
예시를 보자. frac bit의 크기가 3이라고 가정하자.
| 값 | M | GRS | 반올림 여부 | 결과 |
| 128 | 1.000 0000 | 000 | N | 1.000 |
| 15 | 1.101 0000 | 100 | N | 1.101 |
| 17 | 1.000 1000 | 010 | N | 1.000 |
| 19 | 1.001 1000 | 110 | Y (round-to-even) | 1.010 |
| 138 | 1.000 1010 | 011 | Y | 1.001 |
| 63 | 1.111 1100 | 111 | Y | 10.000 |
반올림 결과로 발생하는 overflow
위 예시에서 63을 보자. 반올림 전에는 1.111 1100이었는 반올림 후에는 10.000이 되어 버렸다. 이렇게 되면 E에 1을 더해 주어야 하며, 그 결과로 overflow가 발생할 수도 있다.
변환 예시
변환 예시 : Number to Floating Point
1/3을 floating point로 표현해 보자. 위에서 언급된 방법을 따라보자.
- 수를 2진수의 급수 형태로 표현한다.
- 1/3 = 0.3333 = 1/4 + 1/16 + 1/64 + ... = 0.010101...$_2$이다.
- (-1)$^s$M2$^E$ 형식으로 변환한다.
- 0.010101...$_2$은 1.0101...$_2$ * 2$^{-2}$이다.
- 정해진 bit의 개수에 따라 bias를 구하고, E와 bias를 이용해 exp bit를 구한다. 이 때 rounding을 하며, overflow 발생 시 exp값을 조정한다.
- float는 exp가 8bit, frac이 23bit이다. E = -2, bias = 2$^{7}$ -1 = 127이므로 exp = bias + E = 125, 따라서 exp bit는 0111 1101$_2$이다.
- M값으로 frac bit를 구한다.
- frac은 0101 0101 0101 ... 이며, rounding 시 G = 0, R = 1, S = 1이므로 roundin한다. 0101 0101 ... 011이다.
| s | exp | frac |
| 0 | 0111 1101 | 0101 0101 0101 0101 0101 011 |
변환 예시 : Floating Point to Number
- 수를 정해진 형식에 따라 sign bit, exp bit, frac bit로 분류한다.
- sign bit = 1, exp bit = 0111 1101$_2$, frac = 0101 0101 0101 0101 0101 011$_2$이다.
- exp bit, frac bit을 이용해 normalized / denormalized / special 분류를 한다.
- exp bit가 000..00 또는 111..11이 아니므로 normalized이다.
- exp bit로 E값을, frac bit로 M값을 구한다.
- E = exp - bias에서 exp = 125, bias = 2$^{7}$ -1 = 127이므로 E = -2이다.
- frac = 0101 0101 0101 0101 0101 011$_2$이므로 M = 1.01010101010101010101011이다.
- (-1)$^s$M2$^E$에 값을 넣어 수를 구한다.
- 1.01010101010101010101011$_2$ * 2$^{-2}$ = 0.0101010101010101010101011$_2$ = 0.3333333432674407958984375이다. C++로 돌려보면 값이 맞게 나온다.
Floating Point의 연산
덧셈이든 곱셈이든, floating point의 연산을 진행한 후 rounding한다.
곱셈
(-1)$^{s1}$M1 * 2$^{E1}$ * (-1)$^{s2}$M2 * 2$^{E2}$ = (-1)$^{s}$M * 2$^{E}$라고 할 때, 결과값은 다음과 같다.
- s = s1 ^ s2
- M = M1 * M2
- E = E1 + E1
만약 연산 결과 M이 1보다 커진다면 E에 1을 더하고, M을 [1.0, 2.0) 범위에 들어가게 재조정하며 이후 M을 rounding한다. 이 과정에서 overflow가 날 수 있다.
덧셈
(-1)$^{s1}$M1 * 2$^{E1}$ + (-1)$^{s2}$M2 * 2$^{E2}$ = (-1)$^{s}$M * 2$^{E}$라고 할 때, 단순히 두 소수를 더한 후 float의 범위에 맞게 재조정하는 과정을 거친다. 마찬가지로 이 과정에서 overflow가 날 수 있다.
몇 가지 문제
x는 signed integer이고, f는 float, d는 double이다. f, d는 INF나 NaN이 아니라고 가정한다.
| 문제 | 결과 | |
| 1 | x == (int)(float) x | false |
| 2 | x == (int)(double) x | true |
| 3 | f == (float)(double) f | true |
| 4 | d == (float) d | false |
| 5 | f == -(-f) | true |
| 6 | 2/3 == 2/3.0 | false |
| 7 | d < 0.0 then d*2 < 0.0 | false |
| 8 | d > f then -f > -d | true |
| 9 | d * d >= 0.0 | true |
| 10 | (d + f) - d == f | false |
- float의 범위가 3.4 * 10$^{38}$이지만 2$^{24}$ 내에서만 정확한 수를 표현할 수 있다. 그러나 signed int는 2$^{31}$까지 올라가기 때문에 다른 값이 튀어나온다. 따라서 false.
- double의 정확도는 2$^{53}$ 범위에서 정확한 수를 표현할 수 있으므로 true.
- double의 정확도와 범위가 더 크므로 항상 값이 유지된다.
- float의 정확도와 범위가 더 작으므로 값이 사라질 수 있다.
- -1을 곱하는 연산은 sign bit만 바뀐다.
- 2/3은 integer이기 때문에 0이다. 2/3.0은 float로 나누기 때문에 대략 0.6 근방의 소수가 나온다.
- overflow가 나는 경우 -INF로 갈 수 있다.
- 비교는 double로 이루어지며, -1을 곱하는 연산은 sign bit만 바뀌므로 overflow가 일어나지 않는다. true.
- d * d는 overflow가 날 수 있으며 +INF가 된다. 그러나 +INF는 항상 0보다 크거나 같다. true.
- d + f가 overflow 날 수 있으며 INF가 된다. 따라서 false.
'CS > OS' 카테고리의 다른 글
| [컴퓨터 SW] Storage - RAM & Disk (0) | 2023.06.14 |
|---|---|
| [컴퓨터 SW] Buffer Overflow (0) | 2023.06.11 |
| [컴퓨터 SW] Array/Structure/Union의 할당과 접근 (0) | 2023.06.11 |
| [컴퓨터 SW] Calling Convention (0) | 2023.06.10 |
| [컴퓨터 SW] Byte Ordering (0) | 2023.06.08 |
![[컴퓨터 SW] Bit를 이용한 컴퓨터의 정보 표현](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FpkfKE%2FbtsjqwFH6QS%2FSYPcWVInrvu6iWSP5yqIK1%2Fimg.png)